Welcome to the another post! We’re taking a nostalgic journey back to elementary school math class. Remember that colorful grid taped on the wall, neatly filled with numbers? That’s right, we’re talking about the good old multiplication chart! It’s far more than just an array of digits.
This timeless tool is a captivating crossroads of learning and discovery, a simple yet powerful way to visualize and understand the basic principles of multiplication. What may initially appear as a dizzying array of numbers is, in fact, a beautifully orchestrated dance of patterns, sequences, and relationships. Strap in and join us as we dive deep into the magic of multiplication charts!
Table of Contents
Multiplication Chart Templates
Multiplication chart templates are valuable educational resources designed to assist students, teachers, and parents in teaching and reinforcing multiplication skills. These templates consist of organized grids that display the multiplication table in a clear and structured manner, making it easier for learners to understand and memorize multiplication facts.
Typically presented as a rectangular table, a multiplication chart template consists of rows and columns. The rows are labeled with multiplicands (numbers being multiplied), while the columns are labeled with multipliers (numbers by which the multiplicands are multiplied). Each cell within the grid represents the product of the corresponding multiplicand and multiplier.
These templates are often available in various formats, including printable versions for physical use or digital versions for online learning and interactive engagement. They can be found in textbooks, educational websites, and educational software, catering to a wide range of learning preferences and needs.
What is a multiplication chart?

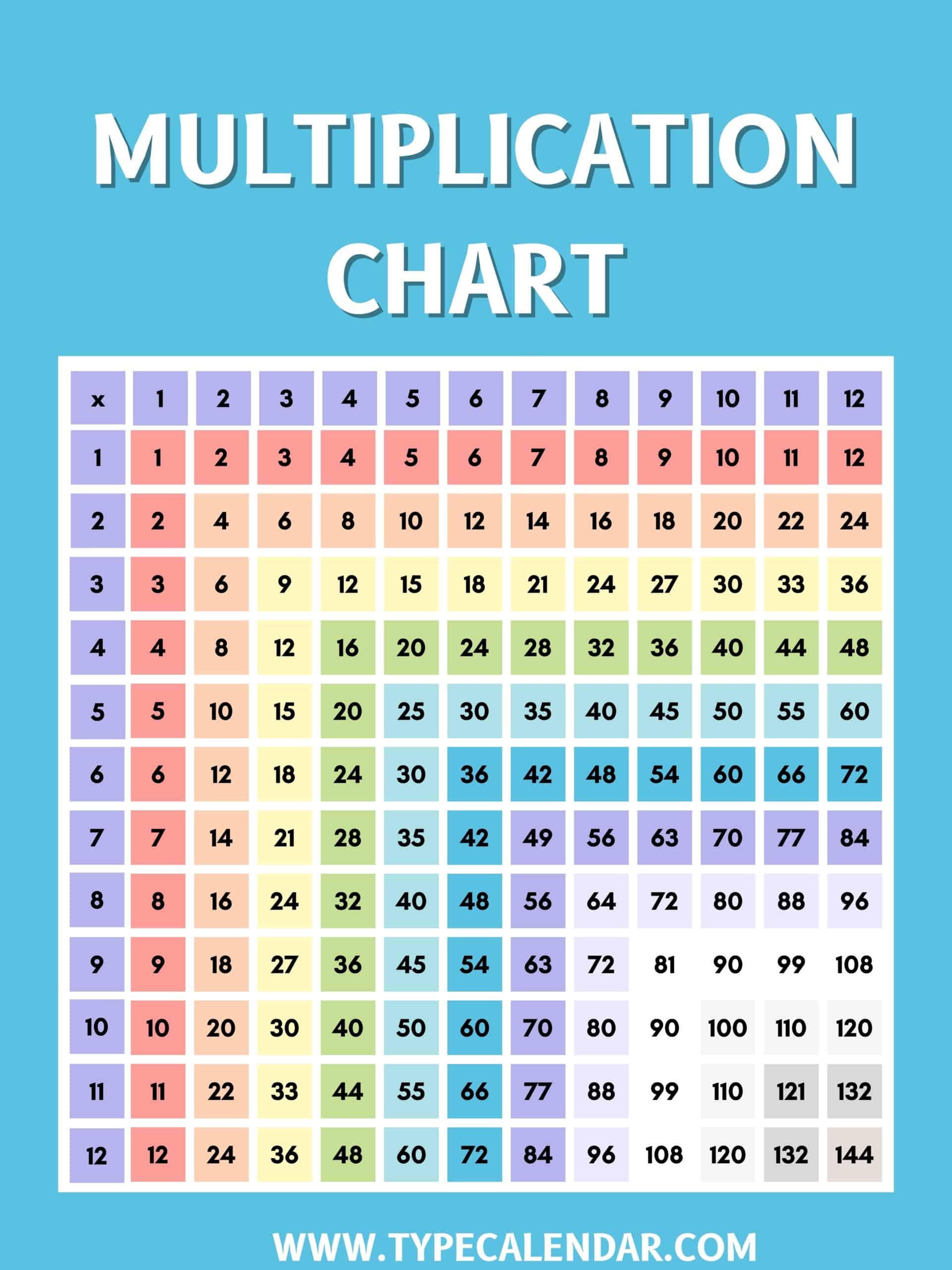
A multiplication chart, often hailed as the unsung hero of early math education, is an effective visual aid designed to simplify the learning and understanding of multiplication. It’s typically a square grid filled with numbers, a straightforward yet powerful tool where rows and columns intersect to display the result of multiplying these two numbers together.
From 1×1 to 10×10 or even larger, a multiplication chart brings to life the fundamental patterns and sequences that form the building blocks of arithmetic. It introduces learners to the beauty of mathematics, demonstrating in a tangible way how numbers relate and interact with each other. Moreover, it’s not just for beginners. More advanced learners often find multiplication charts useful for mastering larger products and developing more sophisticated mathematical skills.
Importance Of Multiplication Chart
Multiplication, an essential arithmetic operation, underpins numerous facets of daily life and academic disciplines, from basic day-to-day calculations to complex problem-solving in fields like engineering, physics, and computer science. A primary educational tool in understanding this fundamental operation is the multiplication chart. This straightforward, yet powerful table presents multiplication facts in an organized and grid-like manner, enabling learners to comprehend and memorize multiplication effectively.
A multiplication chart is a matrix-like structure, wherein rows and columns represent numbers that are to be multiplied together. The intersection point of a specific row and column gives the product of those numbers. This simple structure holds enormous value in learning and understanding the concept of multiplication for numerous reasons. Let’s take a look closer of some benefits of using a multiplication chart:
Grasping Multiplication Concepts
The primary purpose of a multiplication chart is to facilitate a better understanding of multiplication concepts. The tabular representation allows students to discern the patterns and relationships between different numbers. This process aids in conceptualizing multiplication as repeated addition and correlates it to other mathematical operations such as division (as the inverse operation of multiplication). Such a holistic understanding is crucial as it forms the basis for higher mathematical learning and problem-solving.
Aiding Memorization
One of the fundamental aspects of arithmetic learning in the early stages is memorizing basic multiplication facts, typically for single-digit numbers. A multiplication chart plays a pivotal role in this process. By continually referring to the chart, students can memorize these facts, accelerating their arithmetic calculations and building their mathematical confidence.
Pattern Recognition and Analytical Skills
A multiplication chart is filled with numerous patterns. For instance, the products in the diagonal from top left to bottom right are squares of natural numbers, the first row and the first column represent the multiplication of any number by one. Recognizing these patterns is not only fun and engaging for the students but also fosters their analytical thinking and problem-solving skills.
Building Blocks for Higher Mathematics
A strong grasp of multiplication facts, facilitated by the multiplication chart, paves the way for more complex mathematical operations. Concepts such as fractions, algebra, ratios, and proportions all require a solid understanding of multiplication. Therefore, mastery in multiplication, aided by the chart, sets a strong foundation for higher-level mathematics.
Boosting Confidence
Regular practice with a multiplication chart can significantly boost a student’s confidence. As they become faster and more accurate in their multiplication calculations, they become more confident in their abilities. This confidence often translates to better performance in other areas of mathematics and academics as a whole.
Types of Multiplication Chart
Multiplication charts serve as visual aids that can simplify the learning process and make it more engaging. There are several different types of multiplication charts that can cater to different learning styles and needs:
Basic Multiplication Chart
This is the most common type of multiplication chart and is often seen in classrooms. It’s organized as a grid where one set of numbers is listed horizontally across the top and another set of numbers is listed vertically down the side. The cell at the intersection of any row and column will contain the product of the respective row and column numbers.
Blank Multiplication Chart
A blank multiplication chart is an educational tool that allows students to practice their multiplication skills. The chart is formatted the same as a basic multiplication chart, but all the cells are empty. The student’s task is to fill in the cells with the correct products.
Color-Coded Multiplication Chart
This type of chart uses colors to differentiate between different sets of multiples. This visual approach helps students to see patterns and relationships between numbers more easily.
Multiplication Chart with Patterns
This type of multiplication chart highlights patterns in the multiplication tables, which can help students to understand the properties of multiplication and to memorize the tables more easily.
How to Use a Multiplication Chart
A multiplication chart, also known as a times table, is a tool that can be used to learn and remember multiplication facts. It provides a grid of numbers that allows you to find the product of two numbers. Here’s a step-by-step guide on how to use a multiplication chart, followed by an example for more clarification:
Here is Step-by-Step Guide:
Understand the Structure of the Chart
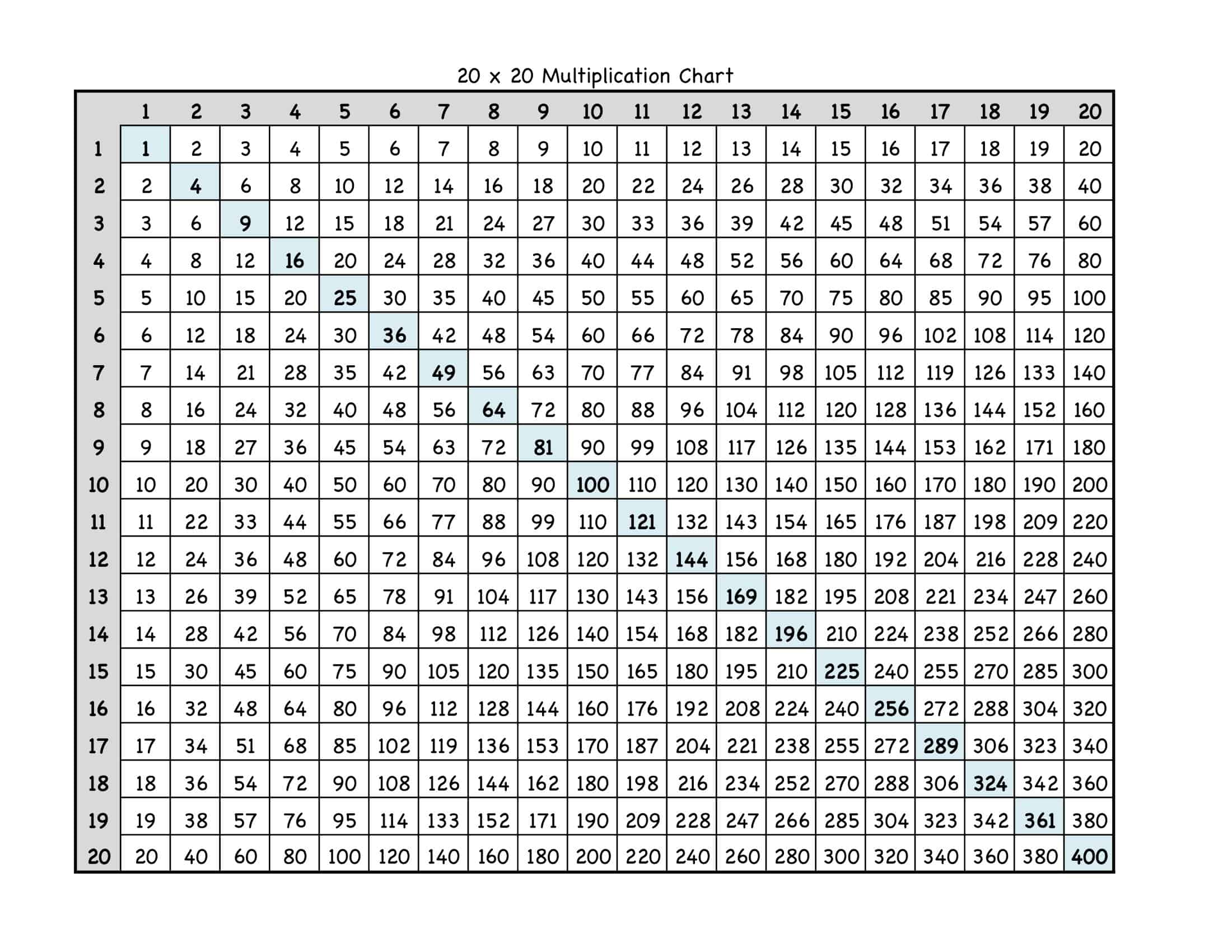
Most multiplication charts are set up as a grid. The top row and the left column usually represent the numbers you’ll be multiplying. For instance, in a 10×10 multiplication chart, the top row and the left column will have numbers ranging from 1 to 10.
Locating the First Number
Once you understand the basic structure, the next step is to locate your first number on the chart. Say you want to multiply 3 by 7. Start by finding the number 3 on the top row of the chart.
Locating the Second Number
Next, you’ll need to find your second number. In this example, the second number is 7. Find it on the left column of the chart.
Follow the Row and Column
After you’ve located both numbers, follow the row across from the first number and the column down from the second number. Where these two intersect on the chart is the product of the multiplication.
Read the Result
The number where the row and column intersect is the result of the multiplication. In our example, the intersection of the row from 3 and the column from 7 gives you the number 21. Therefore, 3 multiplied by 7 equals 21.
Example:
- Let’s say we want to find the result of 5 multiplied by 8.
- Locate the First Number: Find the number 5 on the top row of your multiplication chart.
- Locate the Second Number: Find the number 8 on the left column of your multiplication chart.
- Follow the Row and Column: Trace the row from the number 5 to the right and the column from the number 8 downwards.
- Find the Intersection: Where this row and column intersect is your answer.
- Read the Result: The intersection of the row from 5 and the column from 8 is 40. Therefore, 5 multiplied by 8 equals 40.
Keep in mind that multiplication is commutative, which means you can switch the order of the numbers and the result will be the same (e.g., 5×8 = 8×5 = 40).
Using a multiplication chart is a useful and quick way to learn and remember multiplication facts. As you get more comfortable with it, you’ll find that you can locate products more quickly, improving your overall numerical fluency.
How to Memorize Multiplication Tables – Effective Tips
Memorizing the multiplication table can be a helpful skill, especially for quickly performing calculations in school or in daily life. Here are some detailed steps to memorize it effectively, along with an example to help illustrate the process:
Step-by-step Guide:
- Understand the Basics of Multiplication: Before you start memorizing the multiplication table, you need to understand what multiplication actually is. It’s repeated addition. For example, 2 x 3 is the same as adding 2 three times (2 + 2 + 2).
- Start Small: Start with the 1 times table, even though it’s the easiest (since 1 times any number is always that number). This helps you get used to the idea of the table itself and the patterns within it.
- Proceed in Order: After the 1 times table, proceed to the 2 times table, then 3 times, and so on. It’s typically easier to start in order, as each step up adds a new level of complexity.
- Utilize Patterns and Rules: There are some patterns and rules that can help you memorize the table. For instance, any number times 2 is just the number doubled, any number times 0 is 0, and any number times 1 is itself. For even numbers, there’s a pattern in the 2 times table (2, 4, 6, 8, 10, and so on).
- Break It Down: Break down the table into smaller, more manageable chunks. It’s easier to memorize the table one row at a time, rather than trying to learn the whole thing at once.
- Use Flashcards: Write the multiplication problems on one side of a flashcard, and the answer on the other side. This method promotes active recall, which is a proven method for memorization.
- Practice Regularly: Like any other type of memorization, learning the multiplication table takes regular practice. Spend some time each day reviewing the parts of the table you’ve learned, and adding new parts.
- Test Yourself: After you’ve spent some time memorizing, test yourself to see what you remember. This can show you where your strengths are and where you still need some work.
- Make it Fun: Turn it into a game. You can find online games that help you practice multiplication, or make up your own game with a friend or family member.
Example:
Let’s say you’re working on memorizing the 5 times table.
- Start Small: Understand that 5 x 1 is the same as adding 5 once, so it’s 5.
- Proceed in Order: Move to 5 x 2, which is the same as adding 5 twice (5 + 5), so it’s 10.
- Utilize Patterns and Rules: As you continue, you might notice that the last digit of the 5 times table alternates between 5 and 0.
- Break It Down: Work on the 5 times table by itself until you have it memorized.
- Use Flashcards: On one side of a flashcard, write 5 x 6. On the other side, write 30. Use this to help you memorize the fact.
- Practice Regularly: Practice the 5 times table every day, adding more multiplication facts as you get comfortable with the ones you’ve learned.
- Test Yourself: Once you feel confident, test yourself on the 5 times table. Can you remember all the multiplication facts up to 5 x 10?
- Make it Fun: Play a game where you roll a die, and whatever number you roll, you have to multiply it by 5. For example, if you roll a 6, you would say “30” because 5 x 6 equals 30.
As a final tip, make sure you understand and can use the multiplication facts, not just recite them. The ultimate goal isn’t just memorizing the table, but being able to use it to solve problems and perform calculations. If you’re just starting to learn, don’t worry if it seems hard or if you make mistakes – this is completely normal. The more you practice, the better you’ll get.
Determining the Optimal Grade for Introducing Multiplication Chart to Children
Children typically begin learning multiplication in the early elementary grades, usually around 2nd or 3rd grade, depending on the educational system and curriculum. At this stage, they have already developed a solid foundation in basic arithmetic, including addition and subtraction. Introducing multiplication at this point allows children to build upon their existing mathematical knowledge and expand their understanding of numbers and operations.
In the initial stages, children are usually introduced to multiplication through arrays, repeated addition, or using manipulatives like counters or blocks. They learn to recognize patterns and relationships between numbers, gradually progressing to memorizing multiplication facts and understanding the concept of multiplication as a shortcut for repeated addition.
As children progress through elementary school, they continue to refine their multiplication skills, learning strategies such as skip counting, using number lines, and applying multiplication in real-life contexts. They also start to work with larger numbers and explore more complex multiplication concepts, such as multiplying by multiples of ten or multiplying three or more factors.
By the end of elementary school or early middle school, most children are expected to have a solid grasp of multiplication facts up to at least 10×10 and be able to apply multiplication to solve various mathematical problems. However, it’s important to note that each child learns at their own pace, and some may require additional support or practice to master multiplication concepts fully.
To sum up, children typically begin learning multiplication in 2nd or 3rd grade, gradually progressing from basic understanding to memorization of multiplication facts and application of multiplication in various contexts. The specific grade at which multiplication is introduced may vary slightly depending on the educational system, curriculum, and individual student readiness.
Multiplication Chart (1-10)
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
FAQs
How to use a multiplication chart to solve problems?
When you encounter a multiplication problem, you can refer to the multiplication chart. Find the numbers you are multiplying on the top row and the left column, and the intersection of their corresponding row and column will give you the answer.
Is a multiplication chart useful for all ages?
While multiplication charts are primarily used for teaching multiplication to elementary school students, they can be a helpful resource for older students and adults who need a quick reference or are working on improving their arithmetic skills.
How to make a multiplication chart?
To make a multiplication chart, draw a square grid. Write numbers 1 to 10 (or 12, depending on how far you want to go) across the top row and down the first column. Then, fill in each square by multiplying the number at the top of the column with the number at the beginning of the row.
Can a multiplication chart help with division?
Yes, a multiplication chart can also help with division. If you know the product and one of the multiplication factors, you can find the other factor on the chart. For instance, if you’re trying to find out what number you need to divide 9 by to get 3, you would look for 9 in the chart and then find 3 in the same row or column.
Is there a multiplication chart for larger numbers?
While the most common multiplication charts cover numbers up to 10 or 12, you can find or create charts that cover larger numbers. It might be less common to see them because they can be quite large and harder to use effectively.
Are there interactive multiplication charts online?
Yes, there are numerous interactive multiplication charts available online. These resources often include games, puzzles, and tests to help learn and memorize multiplication facts.
Are multiplication charts available in different formats?
Yes, multiplication charts are available in various formats such as posters, printable PDFs, online interactive tables, mobile apps, etc. They can be colorful, black and white, large, small, etc., based on learning needs and preferences.
What are the benefits of a color-coded multiplication chart?
A color-coded multiplication chart can help differentiate between different groups of numbers, making the patterns within the multiplication chart more apparent. This can aid in understanding and memorizing multiplication facts.
Are multiplication charts necessary for learning multiplication?
While multiplication charts are a very helpful tool for many students when first learning multiplication, they are not the only way to learn. Strategies like repeated addition, using arrays, and understanding the properties of numbers and multiplication can also be effective.
How to teach kids to use a multiplication chart?
Start by explaining the structure of the chart and how the numbers correspond to each other. Have them follow along the rows and columns to find the product of two numbers. Encourage them to use the chart to answer multiplication questions, gradually helping them to memorize the facts.
Can a multiplication chart help with learning square roots?
Yes, a multiplication chart can help with understanding square roots. A square root of a number is a value that, when multiplied by itself, gives the original number. You can find this pair of identical factors in a multiplication chart.
Are there multiplication charts for fractions and decimals?
While less common, there are indeed multiplication charts available for fractions and decimals. They can be a useful tool for understanding these more complex multiplications.
How can I make learning with a multiplication chart more fun?
To make learning more fun, try turning it into a game. For instance, cover a part of the chart and see if the student can guess the hidden numbers. Or, time how fast they can find the product of a given pair of numbers. Online interactive multiplication charts often include such features.











































![Free Printable Pie Chart Templates [Excel, PDF, Word] Maker 1 Pie Chart](https://www.typecalendar.com/wp-content/uploads/2023/06/Pie-Chart-150x150.jpg 150w, https://www.typecalendar.com/wp-content/uploads/2023/06/Pie-Chart-1200x1200.jpg 1200w)
![%100 Free Hoodie Templates [Printable] +PDF 2 Hoodie Template](https://www.typecalendar.com/wp-content/uploads/2023/05/Hoodie-Template-1-150x150.jpg)
![Free Printable Food Diary Templates [Word, Excel, PDF] 3 Food Diary](https://www.typecalendar.com/wp-content/uploads/2023/05/Food-Diary-1-150x150.jpg 150w, https://www.typecalendar.com/wp-content/uploads/2023/05/Food-Diary-1-1200x1200.jpg 1200w)
