Primes, the building blocks of mathematics. These special numbers have fascinated mathematicians and laypeople alike for millennia. Only divisible by one and themselves, prime numbers unveil intricate patterns and relationships as you map them on the number line.
In this article, we will explore some of these fascinating properties and patterns of prime numbers with the help of charts and graphs. You’ll learn how to easily spot primes, analyze their distribution, and visualize their occurrence along the number line. We’ve created a handy printable prime number chart highlighting primes up to 1000. Use it as a quick reference guide or share it with your math students. Read on to uncover the secrets of these mathematical gems.
Table of Contents
What is Prime Numbers?

Prime numbers are a foundational concept in mathematics, representing numbers that are greater than one and have no divisors other than one and themselves. This means they cannot be formed by multiplying two smaller natural numbers together. For example, 2, 3, 5, 7, 11, and 13 are all prime numbers.
By contrast, numbers that have more than two divisors (1 and themselves) are called composite numbers. Prime numbers have special properties that make them the building blocks of mathematics. The study of prime numbers has intrigued mathematicians for centuries due to their unique properties and patterns.
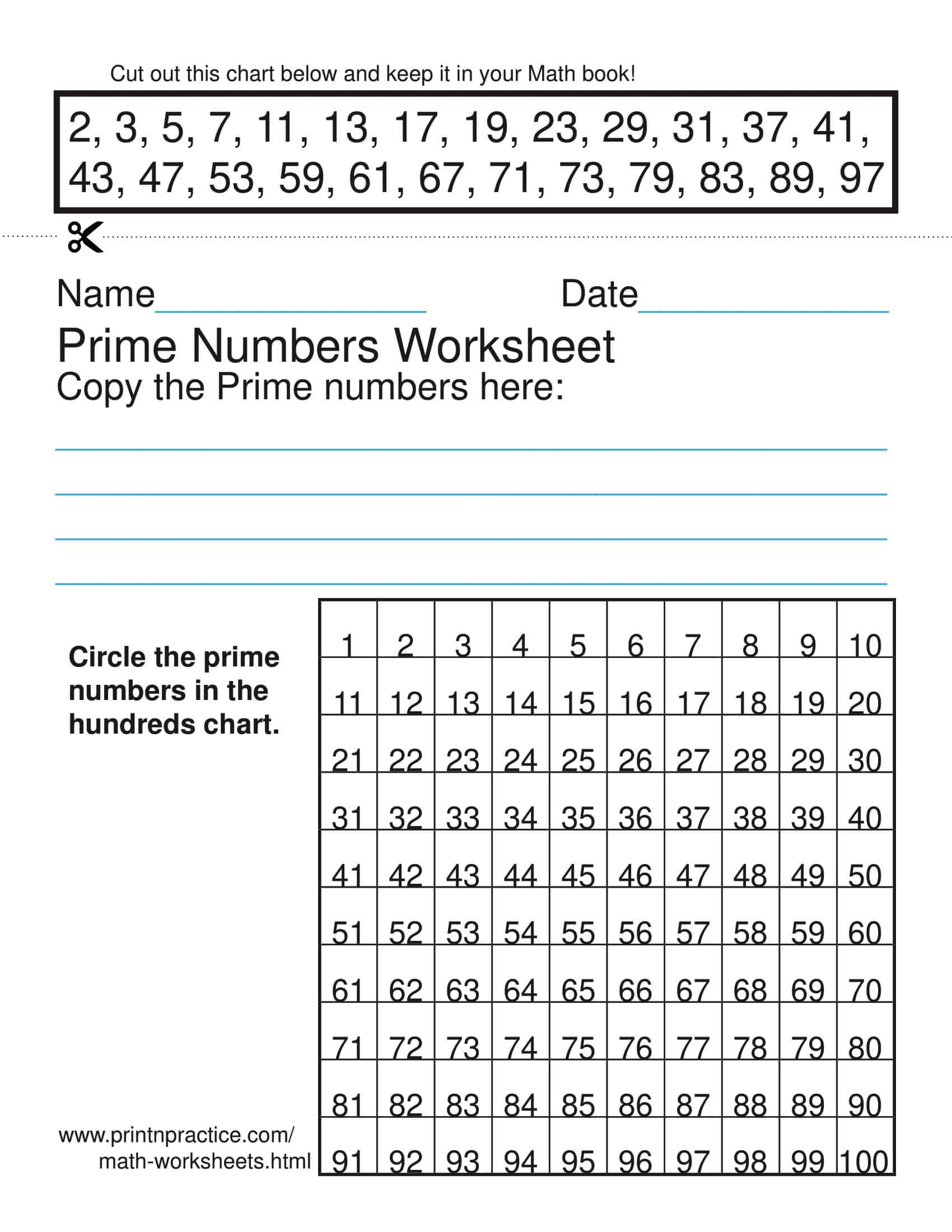
Printable Prime Numbers Chart [1 to 100, 1 to 1000]
Prime numbers are numbers that are only divisible by 1 and themselves. Some examples of prime numbers are 2, 3, 5, 7, 11, 13, etc. Prime numbers are important in many areas of mathematics like cryptography. Prime number charts are helpful visual tools to see and understand patterns of prime numbers.
Prime number chart templates allow you to easily create prime number charts. These chart templates have the basic format and design already made. All you need to do is input the prime numbers you want to display. Chart templates come in many styles like line charts, bar charts, pie charts and more. Some templates are interactive allowing you to highlight or click on individual prime numbers. The templates are customizable too – you can change colors, fonts, sizes etc.
With prime number chart templates you don’t have to build a chart from scratch. The templates make it fast and simple. They help visualize prime number patterns clearly. Teachers or students can print/download attractive prime number charts to display. There are templates suitable for projects, reports, lessons on prime numbers. The pre-made chart templates with prime number data are a useful resource.
Historical Significance of Prime Numbers
The study of prime numbers has fascinated mathematicians for over two millennia. Their seemingly random distribution intrigued ancient Greek mathematicians like Euclid and Eratosthenes who devised the sieve method to detect primes. The quest to understand and predict prime patterns led to major developments in number theory by mathematicians like Gauss and Riemann. Primes play a pivotal role in fundamental theorems of arithmetic that establish the unique prime factorization of integers.
This property underlies public-key cryptography systems like RSA which enables secure communication online. Understanding primes even has implications for the Riemann hypothesis – an unsolved millennium problem with connections to the distribution of prime numbers. Their role in everything from cryptography to nature’s patterns gives prime numbers immense historical significance. Major milestones in our understanding of primes have led to breakthroughs in modern mathematics and still hold valuable insights waiting to be uncovered.
Importance of Prime Numbers
Prime numbers, the indivisible figures of mathematics, hold a position of significant importance in the vast world of numbers. Let’s uncover the multifaceted roles they play across different fields and their historical significance.
1. Foundation of Arithmetic:
- Building Blocks: Just as the periodic table’s elements serve as the fundamental building blocks for all matter, prime numbers are the building blocks of all natural numbers. Through the Fundamental Theorem of Arithmetic, every integer greater than 1 can be uniquely expressed as a product of prime numbers.
2. Cryptography:
- RSA Algorithm: One of the most popular and widely used cryptographic protocols is RSA (Rivest-Shamir-Adleman). It relies heavily on the properties of prime numbers, especially large ones. The difficulty of factorizing the product of two large prime numbers ensures the security of RSA encrypted data.
- Public Key Infrastructure: Many public key systems, including digital signatures and secure socket layer (SSL) for web browsers, rely on the mathematical properties of prime numbers.
3. Error Detection and Correction:
- Coding Theory: Prime numbers are instrumental in coding theory, which is concerned with transmitting data across noisy channels while detecting and correcting errors. They play a pivotal role in designing efficient error-correcting codes.
4. Computer Algorithms:
- Hash Functions: Many algorithms and data structures, like hash tables, use prime numbers to distribute values uniformly. Using primes can reduce the likelihood of ‘collisions’ (two different inputs producing the same output) in these algorithms.
5. Signal Processing:
- Frequency Analysis: In signal processing, prime numbers are used in algorithms that deal with frequency analysis. They can help in minimizing interference and ensuring clearer signal transmission.
6. Nature and Patterns:
- Biological Systems: Some researchers have found patterns that suggest prime numbers play a role in the way certain organisms behave or evolve, like the life cycles of cicadas.
- Randomness & Predictability: Although prime numbers appear to be randomly distributed, they do follow certain patterns and rules. Their study can help bridge the understanding between predictability and randomness in various systems.
7. Historical & Cultural Significance:
- Ancient Civilizations: The ancient Greeks, including mathematicians like Euclid, were fascinated by prime numbers. Their properties and patterns have been the subject of study for millennia.
- Mystical Associations: In various cultures, prime numbers have been associated with mysticism, mainly because of their indivisible nature. They’ve been seen as symbols of purity and indivisibility in different philosophical and religious teachings.
8. Open Problems and Research:
- Riemann Hypothesis: One of the most famous unsolved problems in mathematics, the Riemann Hypothesis, is centered on the distribution of prime numbers. This problem, if solved, could greatly deepen our understanding of primes.
- Prime Gaps: Understanding the gaps between consecutive prime numbers is a hot research topic. While we know that there are infinitely many primes, the nature of their distribution remains a tantalizing mystery.
Characteristics of Prime Numbers
Prime numbers are among the most enigmatic entities in the field of mathematics. They are unique, and their properties have fascinated scholars and mathematicians for ages. Let’s delve deeper into their intriguing characteristics, with a special focus on their uniqueness and the Fundamental Theorem of Arithmetic.
1. Uniqueness of Prime Numbers:
- Definition: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This means no prime number can be written as a product of two smaller natural numbers.
- Distinctiveness: Every prime number is unique. No two distinct sets of prime numbers will have the same product. For instance, the only set of prime numbers that can be multiplied to give a product of 15 is 3 and 5.
- Infinite Nature: One of the foundational results in mathematics, proven by Euclid over two millennia ago, is that there are infinitely many prime numbers. No matter how large a prime number you find, there will always be another prime number greater than it.
2. The Fundamental Theorem of Arithmetic:
- Statement: Every integer greater than 1 can be uniquely expressed as a product of prime numbers, up to the order of the factors. This means that there’s only one set of prime numbers that, when multiplied together, will result in that number.
- Implications:
- Decomposition: Every integer can be broken down, or “decomposed”, into prime numbers. For example, 84=2×2×3×784=2×2×3×7, which are all prime numbers.
- Uniqueness: This decomposition is unique except for the order of the prime factors. Using our previous example, you might also express 8484 as 2×3×2×72×3×2×7 or any other arrangement, but the set of prime numbers (2, 3, and 7) remains the same.
- Applications: This theorem is foundational in number theory, with implications in various branches of mathematics and its applications. For instance, it’s a basic principle behind the RSA encryption system, which forms the backbone of modern cryptographic methods.
Prime Numbers Charts
A Prime Numbers Chart is an incredibly useful tool for both students and mathematics enthusiasts. It offers a structured and easily digestible visualization of these unique numbers. Let’s explore the chart in detail, emphasizing its visual representation and providing a list of prime numbers up to 500.
1. Visual Representation:
- Purpose: The primary aim of a Prime Numbers Chart is to visually display prime numbers, making it easier to identify and differentiate them from composite numbers.
- Structure:
- Typically, the chart is laid out in a grid format, much like multiplication tables.
- Each cell in the grid either contains a prime number or is blank/indicates a non-prime number.
- Some charts may color-code prime numbers to further highlight them, allowing for quicker identification.
- Benefits:
- Quick Reference: Users can rapidly locate and identify primes without having to mentally parse through a list.
- Pattern Recognition: By visualizing primes on a chart, some users may notice patterns or trends, aiding in their understanding and memory of these numbers.
Prime Numbers from 1 to 500
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 |
| 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 |
| 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 | 229 |
| 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 |
| 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 |
| 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 |
Methods for Identifying Prime Numbers
Identifying prime numbers has been a topic of intrigue and significance for millennia. A multitude of methods have been developed over time to determine the primality of numbers. In this guide, we will delve deeply into three primary methods: Trial Division, Sieve of Eratosthenes, and Fermat’s Little Theorem.
1. Trial Division:
- Basic Idea: Trial division involves testing divisibility of a number n by all prime numbers less than the square root of n. If none of them divide n, then n is prime.
- Steps:
- Find the square root of n.
- Test if n is divisible by any prime number less than or equal to this square root.
- If none divides n completely (i.e., the remainder is always non-zero), n is a prime number.
- Efficiency: It’s not the most efficient for large numbers, but it’s straightforward and requires minimal mathematical background.
2. Sieve of Eratosthenes:
- Basic Idea: This ancient algorithm systematically eliminates the multiples of each prime, starting from 2, the first prime number.
- Steps:
- List all integers from 2 to the maximum number n you want to search.
- Start with the first number (2). Eliminate all multiples of 2 from the list.
- Move to the next number (3) and eliminate all its multiples.
- Continue the process until you’ve processed all numbers up to n.
- The remaining numbers in the list are all prime.
- Efficiency: It’s more efficient than trial division for finding all primes up to a certain limit. Its time complexity is O(n log(log(n))).
3. Fermat’s Little Theorem:
- Basic Idea: While it’s not a definitive test for primality, Fermat’s Little Theorem provides a method that can often quickly identify many non-prime numbers. The theorem states that if p is a prime number and a is any integer greater than 1 and less than p, then a^(p-1) mod p will always be 1.
- Steps:
- Pick a random number a between 1 and n-1.
- Compute a^(n-1) mod n.
- If the result is not 1, then n is definitely not a prime. If it is 1, n is probably prime.
- Repeat the test with different values of a to increase confidence.
- Note: If n fails the test, it’s composite. If it passes, it’s prime with a high probability, but not certainly.
- Efficiency: This method is often used as a quick preliminary test before applying a more definitive (but slower) primality test. It’s especially useful when dealing with very large numbers.
Properties of Prime Numbers
For centuries, mathematicians have been fascinated by prime numbers – integers greater than 1 that can only be divided by 1 and themselves. The special qualities of primes have inspired mathematicians to come up with theories, conjectures, and theorems that try to explain their behavior. In this part, we’ll explore some of the captivating properties that make prime numbers so interesting to study and understand on a deeper level.
By looking at primes through the lens of pivotal mathematical ideas, we can gain insight into the patterns and fundamental nature of these unique numbers. Join us as we dive into some of the most intriguing aspects of the primes and what they can teach us about the abstract yet universal realm of mathematics.
1. Goldbach’s Conjecture:
- Basic Idea: Proposed by the German mathematician Christian Goldbach in 1742, this conjecture states that every even integer greater than 2 can be expressed as the sum of two prime numbers.
- Examples:
- 10 = 3 + 7
- 20 = 7 + 13 = 3 + 17
- Status: To date, no one has been able to prove or disprove Goldbach’s Conjecture, despite it being tested and found true for numbers up to 4 x 10^18. It remains one of the oldest unsolved problems in number theory.
2. Twin Primes:
- Definition: Twin primes are pairs of prime numbers that have a difference of 2. Essentially, if p is a prime, then p and p+2 are twin primes if both are prime.
- Examples: (3, 5), (11, 13), (41, 43)
- Twin Prime Conjecture: There’s an assumption that there are infinitely many twin primes. This is based on empirical evidence, but like Goldbach’s Conjecture, it remains unproven.
3. Mersenne Primes:
- Definition: A Mersenne prime is a prime number that can be written in the form M_n = 2^n − 1. Here, n itself must be a prime for M_n to have a chance of being prime.
- Examples:
- When n = 3, M_n = 2^3 – 1 = 7, which is prime.
- When n = 7, M_n = 2^7 – 1 = 127, which is also prime.
- Special Characteristics:
- Mersenne primes have unique properties that make them especially interesting for number theory and computer science.
- Currently, the largest known prime numbers are Mersenne primes, discovered using computer algorithms.
4. Prime Number Theorem:
- Statement: This theorem describes the asymptotic distribution of prime numbers. It states that the number of primes less than a large integer n is approximately n/log(n).
- Implication: As n becomes very large, the probability that a randomly chosen number less than n is prime approaches 1/log(n).
- Proof and History: While observations and conjectures related to the theorem were made by many (including Gauss and Legendre), a rigorous proof was first provided in the late 19th century by Jacques Hadamard and Charles de la Vallée Poussin independently.
Famous Unsolved Problems Related to Prime Numbers
Prime numbers have been the focus of mathematical study for millennia. Despite the extensive research, there are still unsolved problems related to prime numbers that stump the brightest minds. These problems are not just curiosities; they hold deep implications for number theory, cryptography, and computational mathematics. Let’s explore some of these enduring enigmas.
Twin Prime Conjecture
The twin prime conjecture states that there are infinitely many prime numbers that differ by 2. For example, 3 and 5 are twin primes, as are 5 and 7. Despite this seeming pattern, it has not been proven that primes spaced 2 apart go on infinitely. This problem has intrigued number theorists for centuries. In 2013, Yitang Zhang made significant progress by showing that there are infinitely many prime number pairs spaced less than 70 million units apart, but the exactly 2 units apart conjecture remains unsolved.
Goldbach’s Conjecture
Proposed in 1742 by Christian Goldbach, this conjecture states that every even integer greater than 2 can be expressed as the sum of two prime numbers. For example, 6 = 3 + 3, 8 = 3 + 5, etc. Though empirically validated for large numbers, an actual proof has been elusive. In 2013, mathematician Harald Helfgott published a weak version of the theorem, proving that every odd number greater than 5 is the sum of three primes. The general binary Goldbach conjecture, however, is still open.
Legendre’s Conjecture
Made in 1798 by Adrien-Marie Legendre, it states that there is a prime number between n^2 and (n+1)^2 for every natural number n. For example, between 4^2 and 5^2 lie the primes 5 and 7. No exceptions have been found, but Legendre’s conjecture remains unproven. In 2015, Terence Tao made progress by proving the existence of prime gaps below 70 million. Still, the problem for all n remains open.
Polynomial Progressions
Prime numbers seem to follow no polynomial pattern. In 2004, Ben Green and Terence Tao proved the Green-Tao theorem, which states that for any arithmetic progression of the form n + a1k + a2k^2 + … + at*k^t with integer coefficients, there are infinitely many prime values of n. This was a groundbreaking result, but there is no known polynomial that generates exclusively primes. Discovering potential polynomials that yield infinite prime values is an important open problem.
These four unsolved conjectures and questions are at the forefront of prime number research. Mathematicians continue to chip away at them, hoping to uncover properties and patterns that bring us closer to resolving some of the most perplexing mysteries about primes. Their eventual solutions could reveal profound insights into the nature of numbers.
Interesting Facts and Curiosities
Over the years, primes have fascinated mathematicians and the general public alike, leading to the exploration and discovery of many interesting properties, as well as their occurrence in nature, culture, literature, and art.Here are some interesting facts and curiosities about prime numbers:
Largest Known Prime
The largest known prime number is 282,589,933−1, discovered in December 2018 by the Great Internet Mersenne Prime Search (GIMPS). It has 24,862,048 digits and was found by multiplying together two prime numbers discovered earlier by Patrick Laroche. The number belonged to a special class of primes known as Mersenne primes, which have the form 2^P-1 where P is also prime. Discovering new massive primes pushes computational limits and leads to innovations in hardware, software, and mathematics.
Primes in Nature and Culture
Though abstract, prime numbers surprisingly appear in nature. The periodical cicada has life cycles of 13 and 17 years, both primes. This is believed to have evolved to minimize intersection with other cicada broods and avoid predators. Prime numbers show up in man-made constructs too. Musical scales are based on prime number ratios. Western music uses the 12-tone scale, which is made up of the primes 2, 3, and 5. The Unites States flag has 13 stripes (for the original colonies) arranged in prime number rows of 5 and 8.
Primes in Literature and Art
Prime numbers have intrigued great minds for millennia. Euclid proved there are infinitely many primes. Gauss called mathematics the “queen of sciences” and primes “the atoms of arithmetic.” Prime numbers appear in literary works like Mark Helprin’s “A City in Winter,” about attempts to find the largest prime. Graphics artist neo Kaspar uses prime numbers to generate algorithmic art. Prime numbers also influence films, such as the documentary “The Prime Ministers: The Pioneers” about the quest for new primes.
From the abstract world of mathematics to the applied realm of nature and culture, prime numbers continue to fascinate. The qualities that distinguish them from other integers make them a source of inspiration and discovery across disciplines.
FAQs
How are prime numbers charts created?
The simplest method is the Sieve of Eratosthenes. Starting from 2 (the first prime), you mark off all multiples of 2, then move to the next unmarked number (which will be 3) and mark off all its multiples, and so on. The numbers that remain unmarked in the end are prime.
Aren’t there infinite prime numbers? How can you chart them all?
Yes, there are infinitely many prime numbers, a fact proven by the ancient mathematician Euclid. A prime numbers chart can only ever represent a finite section of the primes.
Can a prime numbers chart help in finding prime factors of a large number?
Yes, for relatively small numbers. If you’re trying to find prime factors of a number, you can use the chart to test division by each prime up to the square root of the number in question. For very large numbers, other methods and algorithms would be more efficient.



































![Free Printable Pie Chart Templates [Excel, PDF, Word] Maker 1 Pie Chart](https://www.typecalendar.com/wp-content/uploads/2023/06/Pie-Chart-150x150.jpg 150w, https://www.typecalendar.com/wp-content/uploads/2023/06/Pie-Chart-1200x1200.jpg 1200w)
![%100 Free Hoodie Templates [Printable] +PDF 2 Hoodie Template](https://www.typecalendar.com/wp-content/uploads/2023/05/Hoodie-Template-1-150x150.jpg)
![Free Printable Reward Chart Templates [Word, PDF] Teachers 3 Reward Chart](https://www.typecalendar.com/wp-content/uploads/2023/03/Reward-Chart-150x150.jpg 150w, https://www.typecalendar.com/wp-content/uploads/2023/03/Reward-Chart-1200x1200.jpg 1200w)
