Grasping the distributive property is essential for simplifying expressions and solving equations in algebra. However, many students struggle to remember and accurately apply this fundamental concept. Dedicated practice with the distributive property is key for mastering its use. Distributive property worksheets provide focused exercises and examples to reinforce this vital math skill.
With repetitive practice problems isolating the distributive property, students gain experience distributing terms, simplifying expressions, and solving equations using distribution. In this article, we will explore the benefits of using downloadable distributive property worksheets to cement understanding of this key algebra topic. We provide printable PDF and Word worksheets with step-by-step examples and practice applying the distributive property across a variety of problem types.
Table of Contents
What Is Distributive Property?

The distributive property is a fundamental rule in algebra that involves multiplying a number or variable by the terms inside a grouping symbol or parenthesis. It states that you can distribute a factor across multiple terms inside the parentheses. For example, the distributive property allows you to multiply 3(x+5) as 3x + 15 instead of having to multiply 3 by each term separately.
This property simplifies expressions by allowing you to remove parentheses and groupings and multiply the factor directly with each term inside. The distributive property works with different operations like multiplication and division across terms being added, subtracted, or multiplied. Mastering this property is key for algebra students when expanding expressions, combining like terms, and solving equations. Having fluency with the distributive property helps develop essential abstract reasoning and symbolic manipulation skills.
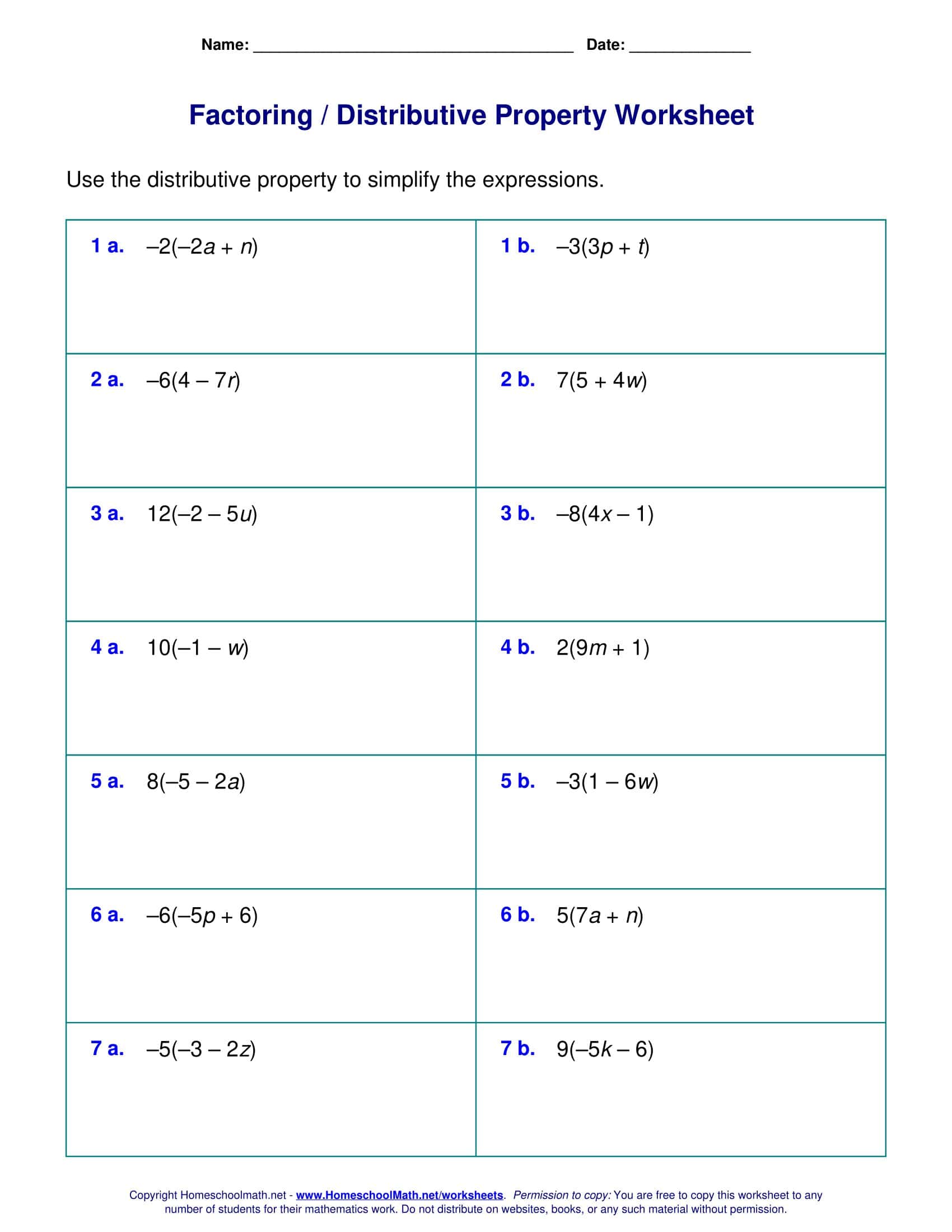
Distributive Property Worksheet Templates
Mastering the distributive property is essential for success in algebra. Our distributive property worksheet pdf provides focused practice with simplifying expressions using distribution. This printable handout includes examples and practice problems to build confidence.
The worksheet starts with clear explanations and examples of distributing variables and constants over addition and subtraction. Students then apply the concepts to evaluate increasingly complex expressions. Step-by-step work is shown for the first few problems before transitioning to independent practice.
This high-quality distributive property worksheet generates much-needed practice on this foundational algebra skill. Students will gain experience simplifying quadratic and polynomial expressions using distribution. The pdf format allows teachers to print and distribute the worksheet for in-class practice or supplemental work. Download our free distributive property worksheet today!
Importance of Distributive Property in Math
The distributive property is foundational for student success in algebra and more advanced mathematics. This property allows mathematical expressions and equations to be simplified and solved through key symbolic manipulation skills. Fluent understanding and application of the distributive property is essential for several reasons.
Firstly, the distributive property is used ubiquitously when expanding algebraic expressions. Students must distribute factors across terms within parentheses and grouping symbols to fully expand expressions. Without the distributive property, expressions would need to be multiplied out term by term, making simplification extremely time-consuming. The distributive property condenses multiple steps into one process, allowing more efficient symbolic manipulation.
Secondly, the distributive property is critical for combining like terms, an essential technique for simplifying algebraic expressions. To combine terms with variables raised to powers, the coefficient must first be distributed to each variable factor. The distributive property enables coefficients to multiply the terms cleanly before bringing together the like variables.
Thirdly, applying the distributive property is often an intermediate step in solving equations. Distributing a term across parentheses or brackets allows the expression to then be combined, isolated, and solved through key algebraic techniques. Using the distributive property facilitates rearranging complex equations into solvable forms.
Finally, fluency with the distributive property supports learning more advanced math concepts and procedures. Manipulating polynomials, rational expressions, and matrices all rely on distribution skills. Mastering this foundational property provides the symbolic manipulation abilities needed for high-level mathematics.
Distributive Property Worksheet Instructions
How to Approach Each Problem:
Start by reading the problem carefully to ensure you understand the terms and what is being asked. Often, the terms within the parentheses will need to be multiplied by a number outside the parentheses. Look for structures similar to “number times (number plus/minus number)”. For instance, if you encounter a problem like “5 times (3 plus 7)”, this indicates a scenario where the distributive property will be applicable.
Break the problem down step by step. Using the example above, begin with the multiplication of the first number outside the parentheses with the first number inside. Next, multiply the number outside with the second number inside the parentheses. Make sure to follow the operations within the parentheses accurately, whether it’s addition or subtraction.
Remember, consistency is key. Once you’ve identified the pattern of distribution in a few problems, you’ll start to recognize it more quickly in subsequent problems. With each problem, practice breaking it down, distributing, and then simplifying to arrive at your final answer.
For example, if the problem reads “6 times (2 plus 8)”, you would multiply 6 by 2, and then 6 by 8, and finally add those two results together.
Recommended Tools and Strategies:
It’s always a good idea to have scratch paper and a pencil handy. This allows you to jot down intermediate steps and ensure that you don’t miss out on any terms during the distribution process. While mental math can be quick, writing down steps helps avoid simple mistakes.
Use color-coding if possible. By highlighting or using different colored pencils for different terms, you can visually keep track of which numbers you’ve already multiplied and which ones are still pending. For example, if you’re working on the problem “7 times (4 plus 9)”, you could color the “7 times 4” multiplication in blue and the “7 times 9” multiplication in red. This visual distinction can help you keep track of your work.
Repetition is beneficial. As you work through multiple problems, you’ll become more familiar with the distribution process, and it will become more intuitive. If you find a particular type of problem challenging, try to find or create similar problems to practice with. The more you practice, the more comfortable you’ll become.
Always double-check your work. After you’ve used the distributive property and arrived at an answer, it can be useful to use the inverse operation to check your work. For instance, if you’ve expanded “8 times (5 plus 3)” and arrived at “40 plus 24”, you can combine those terms and multiply 8 by 8 to see if you get the same result.
How to Use the Distributive Property: A Step-by-Step Guide
To effectively employ the distributive property in mathematical computations, one needs to follow three straightforward steps. These steps provide a clear pathway to break down complex problems, ensuring consistent and accurate results. Whether you’re a budding mathematician or simply looking to sharpen your algebraic skills, grasping the distributive property and its methodical application will prove invaluable.
Step 1: Identify the Expression
Begin by identifying the algebraic expression that requires the application of the distributive property. The expression should typically look like a single term (a number, variable, or coefficient with a variable) outside parentheses, multiplied by two or more terms inside parentheses.
Step 2: Recognize the Structure
Make sure the expression inside the parentheses is an addition or subtraction operation. This structure indicates that the distributive property can be applied. The basic format you’re looking for is something like a(b + c) or a(b – c).
Step 3: Distribute the Outside Term to the First Term Inside
Multiply the term outside the parentheses with the first term inside the parentheses. If our expression is a(b + c), start by multiplying a and b together.
Step 4: Distribute the Outside Term to the Next Term Inside
Now, multiply the term outside the parentheses with the next term inside. Continuing with our expression a(b + c), multiply a and c together. Ensure that you carry the sign (plus or minus) from inside the parentheses through to your resulting terms.
Step 5: Simplify the Expression (if necessary)
After you’ve completed the distribution, combine any like terms in the resulting expression. For example, if after distributing you have an expression like 3x + 5x, combine these to get 8x.
Step 6: Double-Check Your Work
It’s always a good practice to double-check. You can do this by reversing the distribution. If you’ve expanded correctly, you should be able to group the terms back into their original parenthetical expression.
Step 7: Apply to Larger Expressions (Advanced)
In more complex algebraic expressions, there might be more than two terms inside the parentheses, or even nested parentheses. In such cases, apply the distributive property systematically, starting from the innermost parentheses and working your way out. This might require the repeated application of the property.
Example:
Let’s apply these steps to a simple expression: 3(x + 4).
Step 1: Our expression is 3(x + 4).
Step 2: We recognize the structure of one term outside and an addition inside the parentheses.
Step 3: Multiply 3 and x to get 3x.
Step 4: Multiply 3 and 4 to get 12.
Step 5: Combining these results, our expanded expression is 3x + 12.
Step 6: To double-check, if we factor out a 3 from 3x + 12, we get back to our original expression: 3(x + 4).
Step 7: This example does not have larger or nested expressions.
Verification of the Distributive Property
The Distributive Property states that multiplication distributes over addition or subtraction. In mathematical terms, for all real numbers a, b, and c:
a(b + c) = ab + ac … [i]
a(b – c) = ab – ac … [ii]
Let’s verify the distributive property using the above equations.
Verification for Equation [i]:
Given: a(b + c)
To prove: a(b + c) = ab + ac
Proof: LHS (Left Hand Side) = a(b + c) Multiply ‘a’ with each term inside the parenthesis. = a * b + a * c = ab + ac
RHS (Right Hand Side) = ab + ac
Since LHS = RHS, a(b + c) = ab + ac is verified.
Verification for Equation [ii]:
Given: a(b – c)
To prove: a(b – c) = ab – ac
Proof: LHS (Left Hand Side) = a(b – c) Multiply ‘a’ with each term inside the parenthesis. = a * b – a * c = ab – ac
RHS (Right Hand Side) = ab – ac
Since LHS = RHS, a(b – c) = ab – ac is verified.
In both cases, by solving both the LHS and RHS, we have verified the Distributive Property. This property holds true for any real numbers, making it a foundational concept in algebra.
Distributive Property Worksheet: Tips and Common Mistakes
The Distributive Property is a foundational algebraic concept. When working through problems, it’s essential to be aware of potential mistakes and keep certain strategies in mind for success.
Tips for Successful Problem Solving:
- Break It Down: Dissect the equation step-by-step. Identify terms inside the parentheses and the external term.
- Highlight or Underline: On paper, underline or highlight the terms you’re distributing to ensure none are overlooked.
- Work Systematically: Systematically distribute the term outside the parentheses to each term inside.
- Check Your Work: After distributing, combine like terms, which might simplify your expression.
- Practice Makes Perfect: Regular practice makes distributing intuitive and helps in recognizing patterns.
- Use Real-world Examples: Use tangible scenarios like distributing candies among friends to understand the abstract concept.
Pitfalls to Avoid:
- Incomplete Distribution: A common error is failing to distribute the term outside the parentheses to every term inside. For 3(x + 5y), the mistake might be 3x + 5y instead of the correct 3x + 15y.
- Misinterpreting Signs: Be careful with subtraction or negative numbers. For -2(x – 4), the result is 2x + 8, not 2x – 8.
- Over Distributing: Avoid distributing terms when not required. In 3x(4 + y), you shouldn’t distribute the x.
- Confusing Multiplication with Addition: Remember, you’re multiplying the term outside the parentheses with each term inside, not adding them.
- Overcomplicating Expressions: With terms like x(2 + 3y), you don’t need to distribute the x to 2 since 2x is already its simplest form.
- Forgetting Order of Operations: Follow the PEMDAS/BODMAS rule. Address parentheses first, especially if there are operations inside to tackle before distributing.
- Not Combining Like Terms: After distribution, always merge like terms. For an equation like 2x + 3(x + 4) = 5x + 12, after distributing, combine the 2x and 3x to get 5x.
Conclusion
Fluency with the distributive property is pivotal for algebra success. Our printable distributive property worksheets provide extensive practice for applying this fundamental concept across diverse expression and equation types. Repeated practice distributed over time can help students gain proficiency with efficiently multiplying factors across grouped terms and parentheses.
We offer engaging distributive property worksheets available for free download as both PDF and editable Word documents. The step-by-step examples and progressively challenging questions strengthen skills. Use these worksheets to reinforce lessons on the distributive property. Download our materials today and equip students with this foundational algebra ability through consistent practice. Building proficiency will pave the way for algebra mastery.
FAQs
Are there any exceptions to the Distributive Property?
No, the Distributive Property holds true for all real numbers. However, always be cautious about the order of operations and ensure that you distribute correctly.
What’s the difference between the Distributive Property and FOIL (First, Outer, Inner, Last) method?
The Distributive Property is a general principle that applies to all real numbers, while FOIL is a mnemonic specifically used for multiplying two binomials. FOIL is essentially an application of the Distributive Property.
How does the Distributive Property help in real-world situations?
The Distributive Property can be applied to real-life scenarios like splitting costs, distributing resources, or calculating combined rates. It helps in breaking down complex problems into manageable parts.
Is the Distributive Property only applicable to binomials?
No, while it’s often taught initially using binomials, the Distributive Property can be used for expressions with more than two terms as well.








































![%100 Free Hoodie Templates [Printable] +PDF 1 Hoodie Template](https://www.typecalendar.com/wp-content/uploads/2023/05/Hoodie-Template-1-150x150.jpg)
![Free Printable Food Diary Templates [Word, Excel, PDF] 2 Food Diary](https://www.typecalendar.com/wp-content/uploads/2023/05/Food-Diary-1-150x150.jpg 150w, https://www.typecalendar.com/wp-content/uploads/2023/05/Food-Diary-1-1200x1200.jpg 1200w)
![Free Printable Roommate Agreement Templates [Word, PDF] 3 Roommate Agreement](https://www.typecalendar.com/wp-content/uploads/2023/06/Roommate-Agreement-150x150.jpg)
