TypeCalendar has prepared 53+ Pythagorean Theorem worksheets (with answer keys) to explore the world of right triangles ranging from visually supported warm ups to mixed practice, word problems to coordinate plane and 3D extensions all in one pack. Each page is designed to be used in class by photocopying, on the screen as a PDF or as homework, and all include a detailed answer key and step by step solution. TypeCalendar focuses on helping students truly understand the relationship “a² + b² = c²” while saving teachers time.
Table of Contents
What Is a Pythagorean Theorem Worksheet?
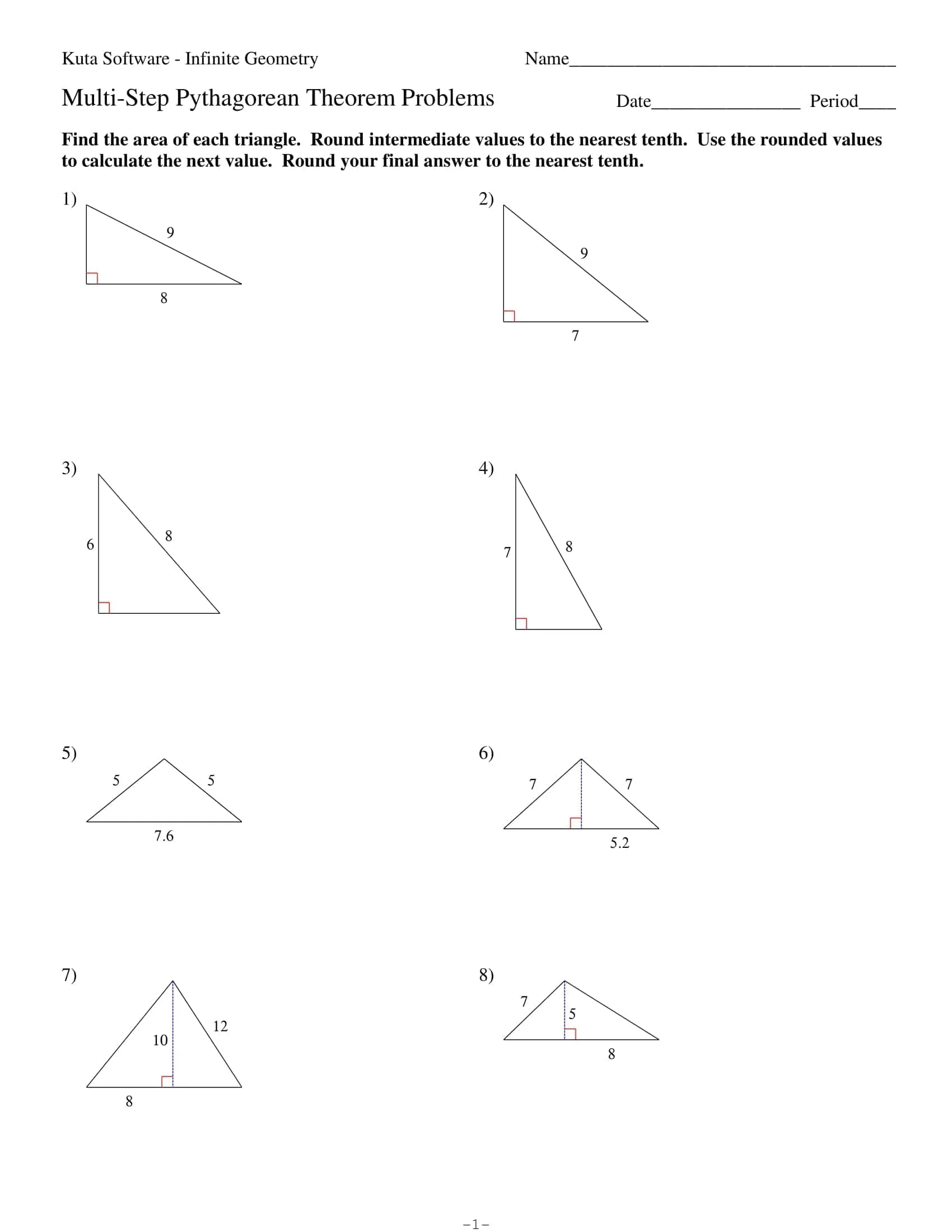
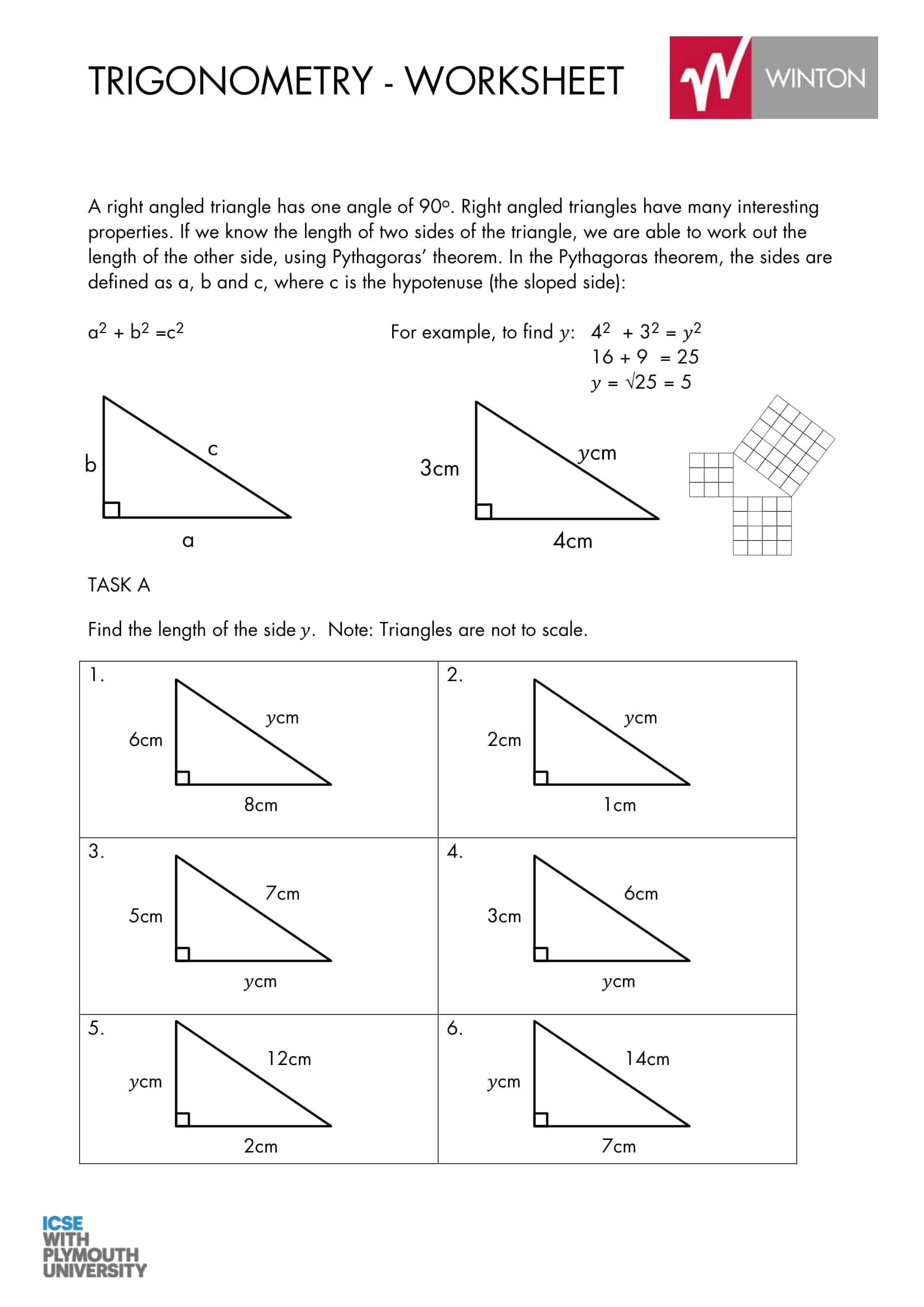
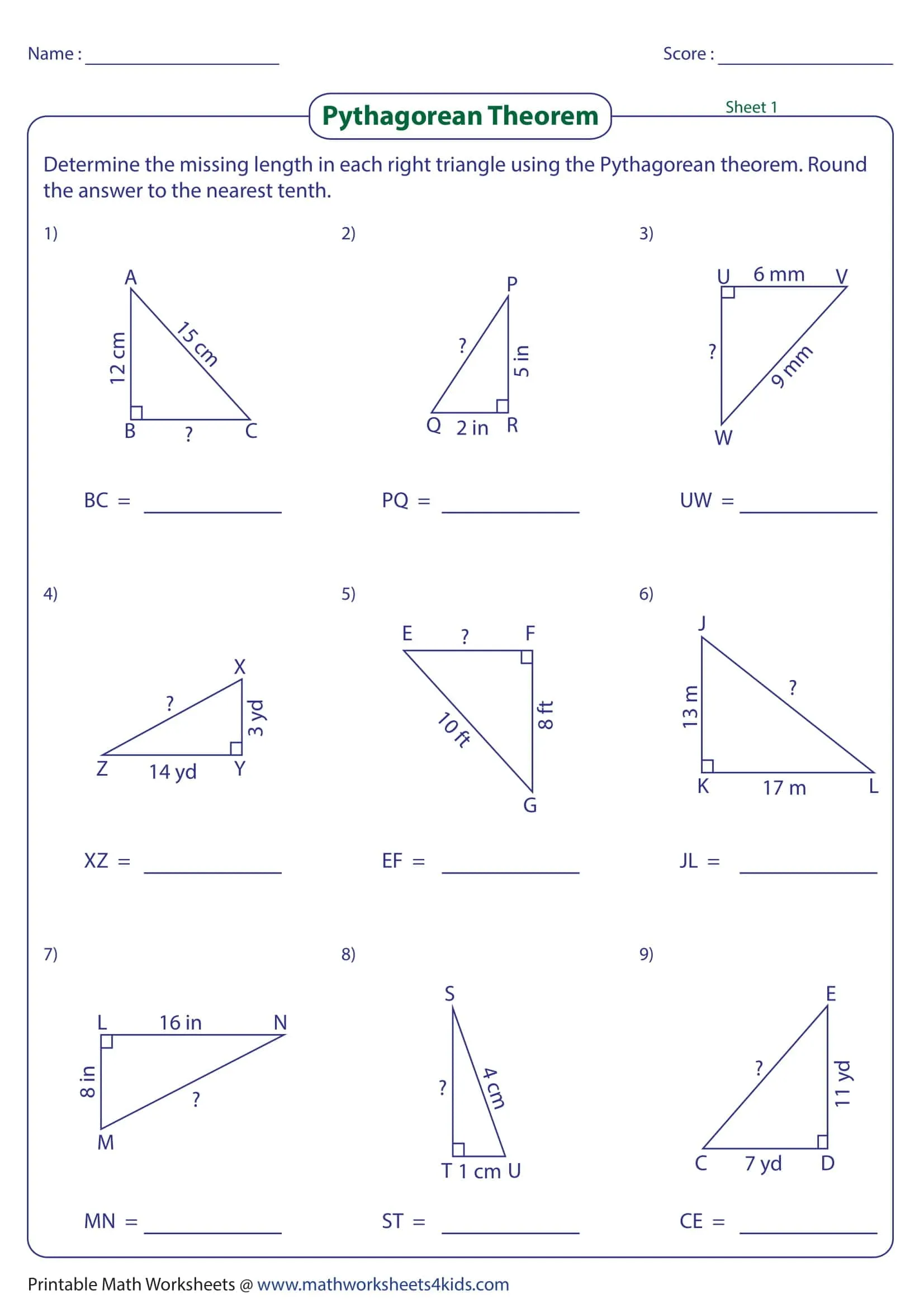
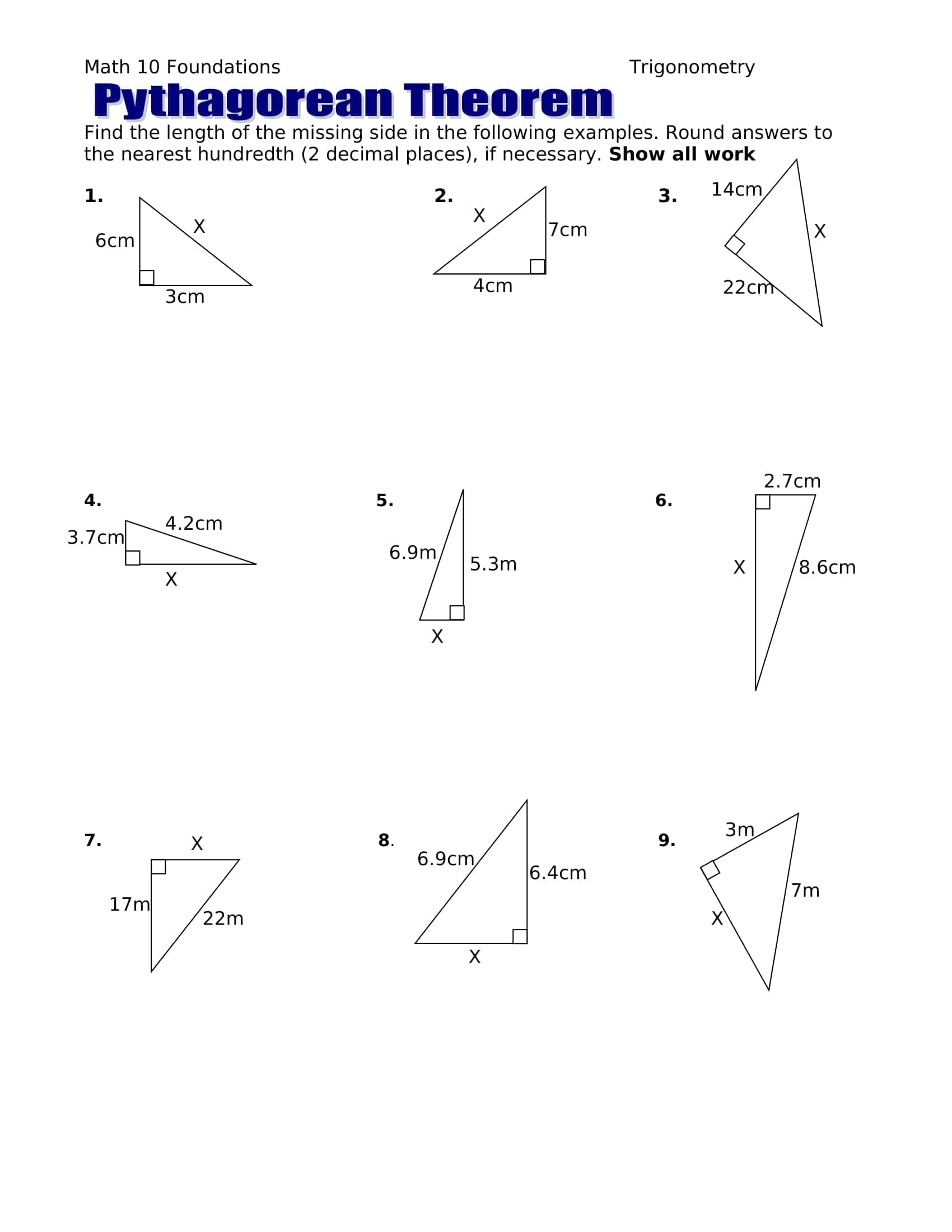
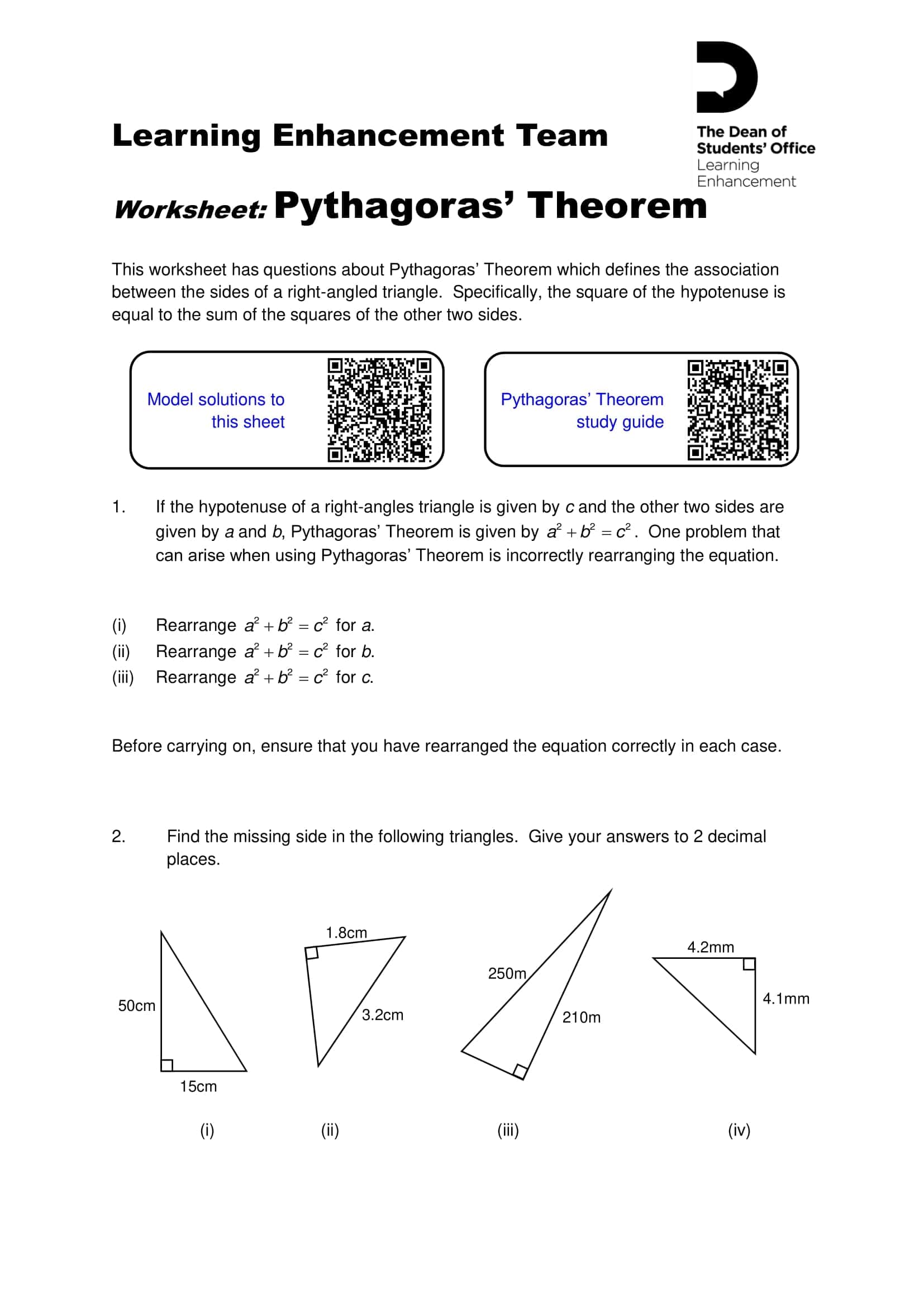
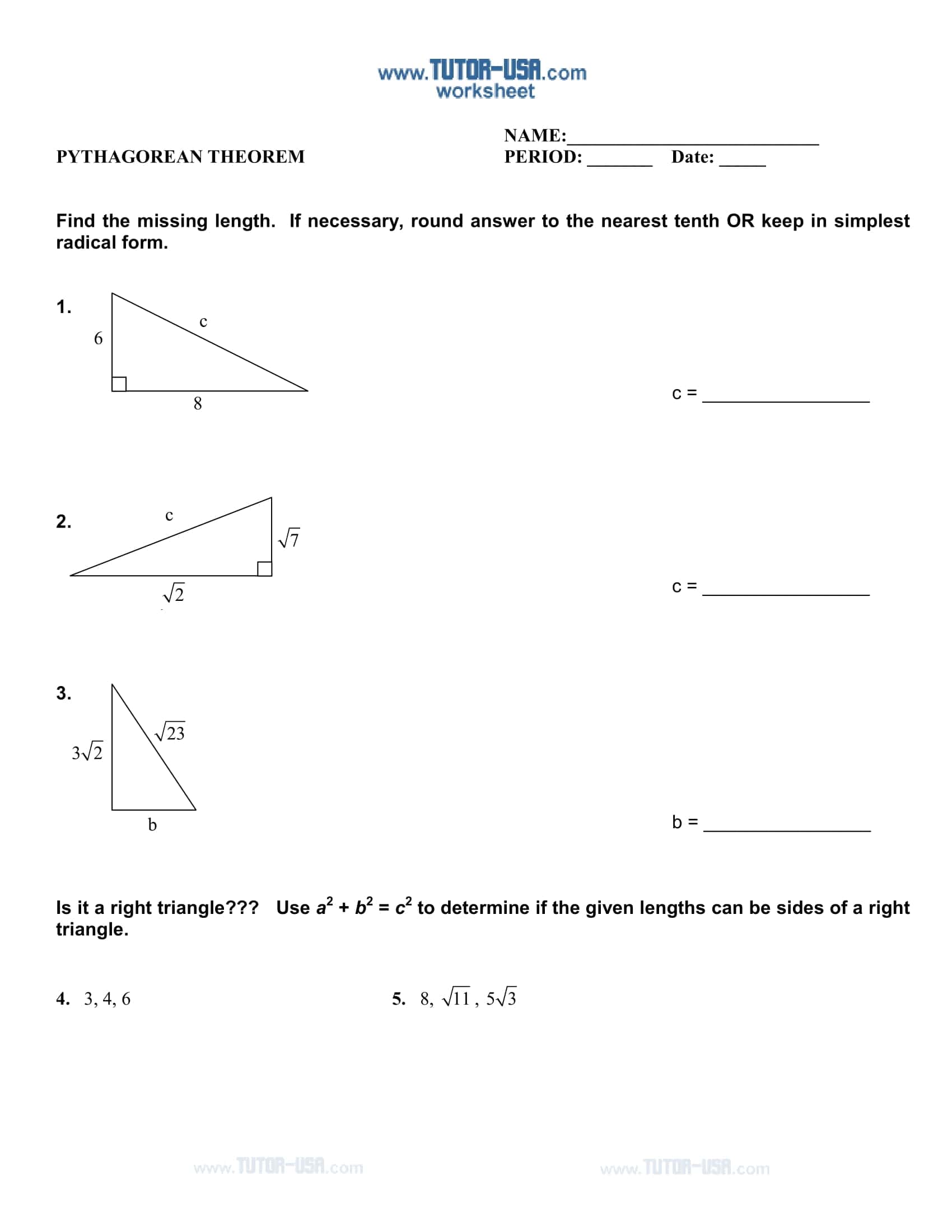
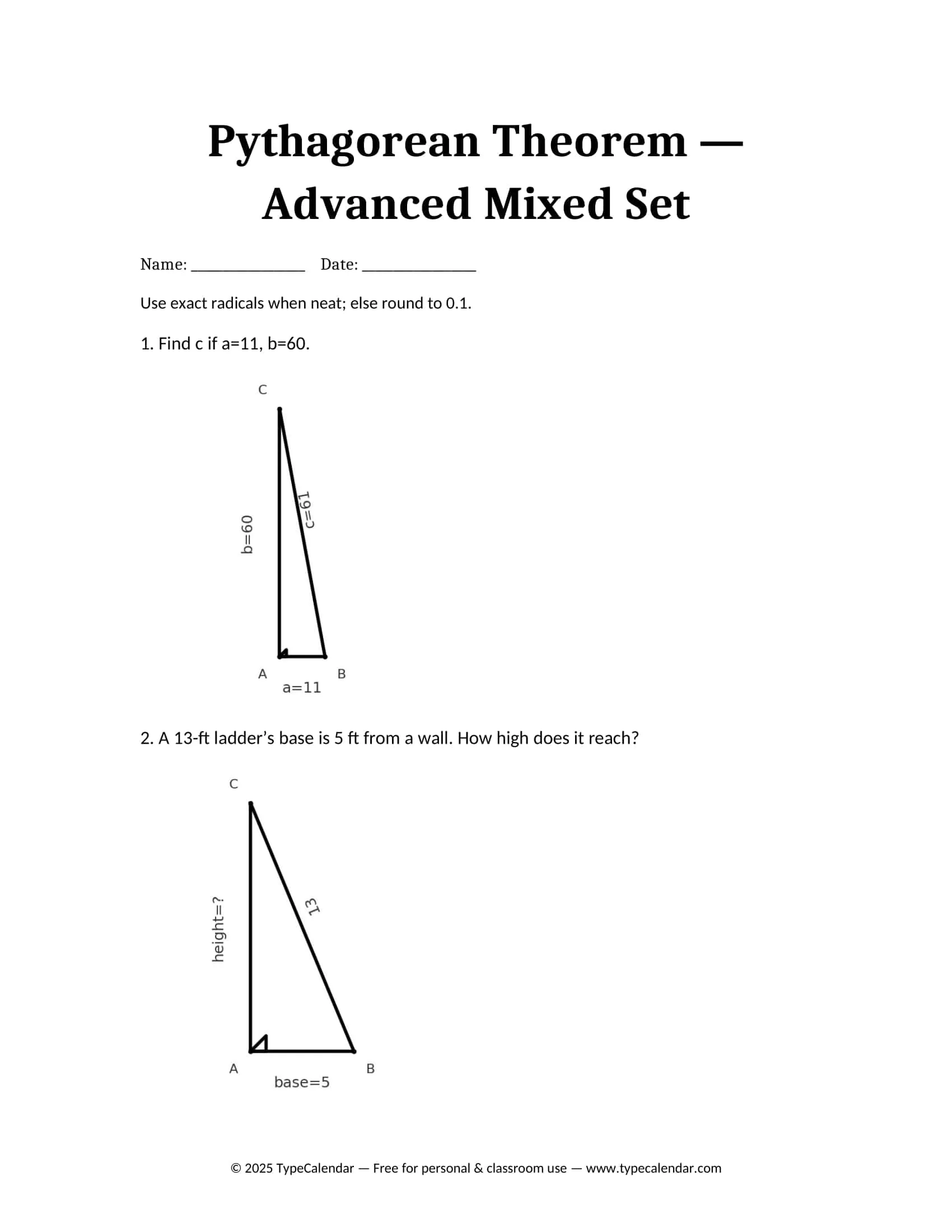
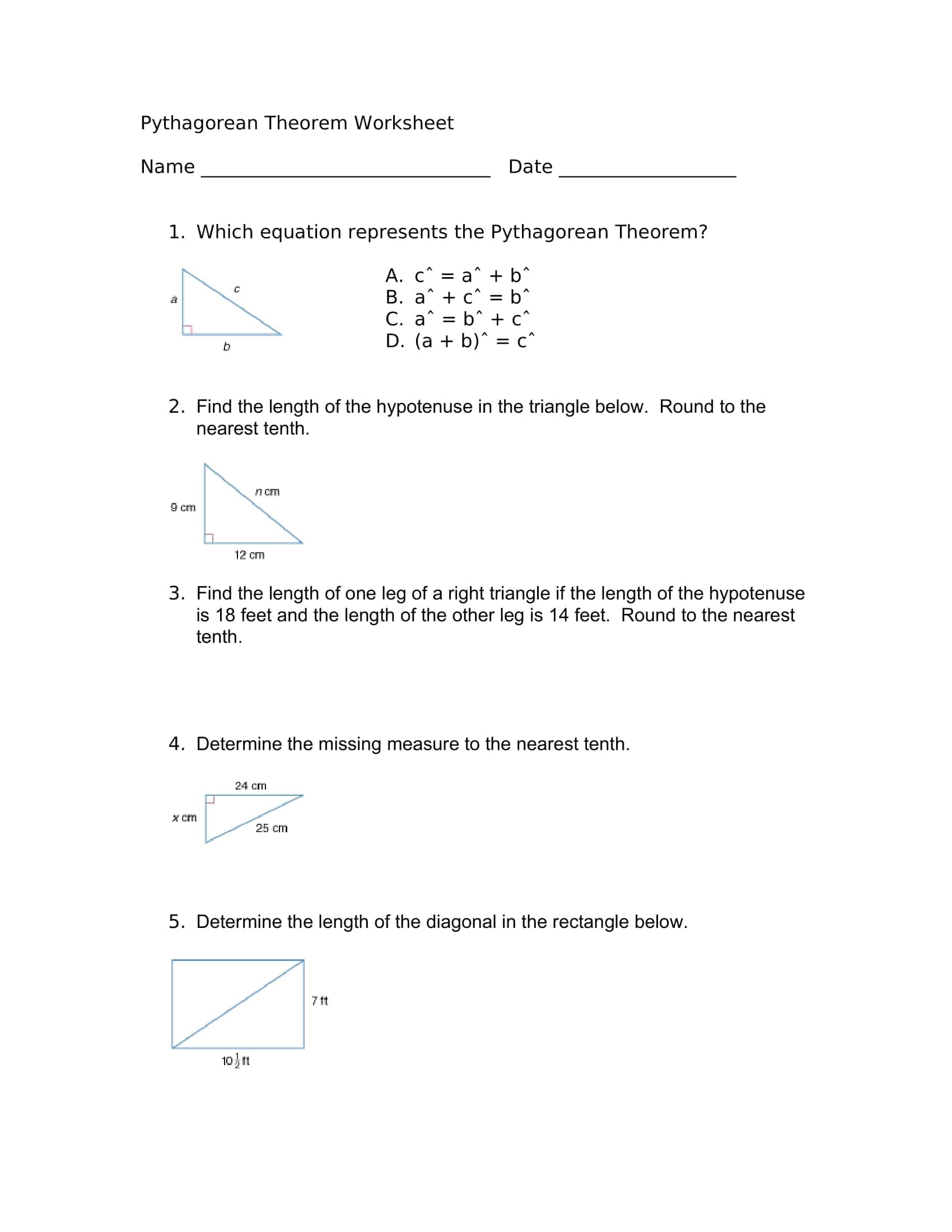
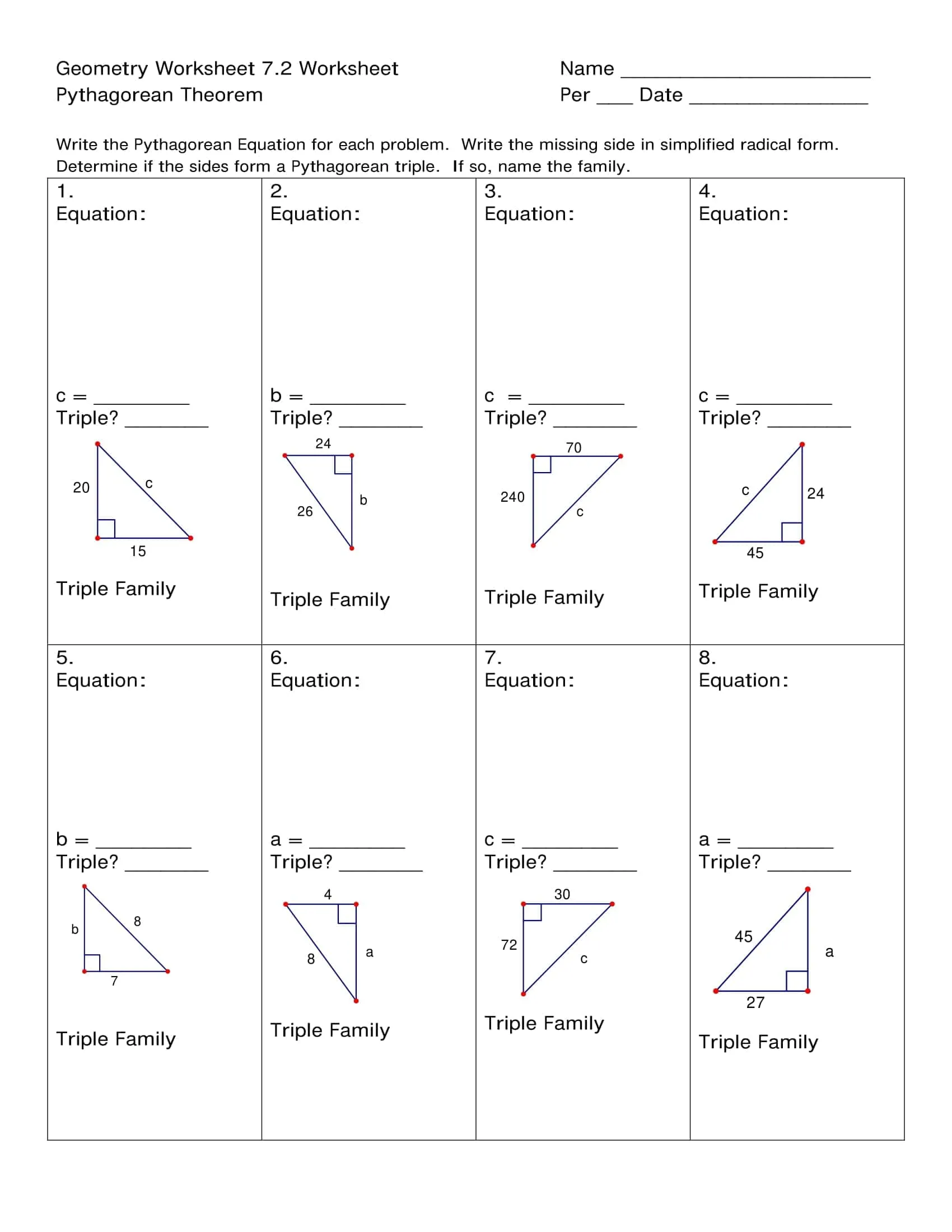
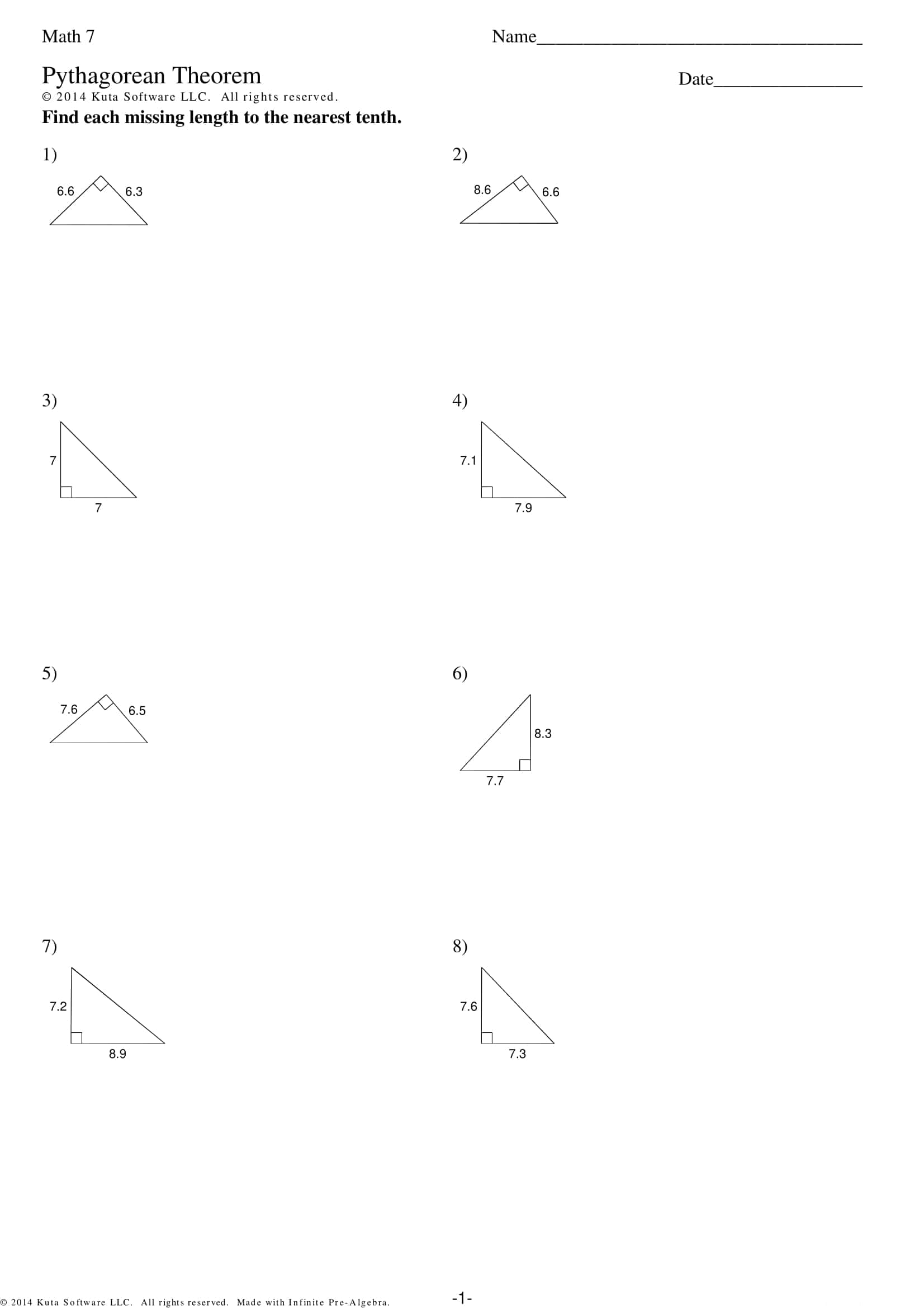
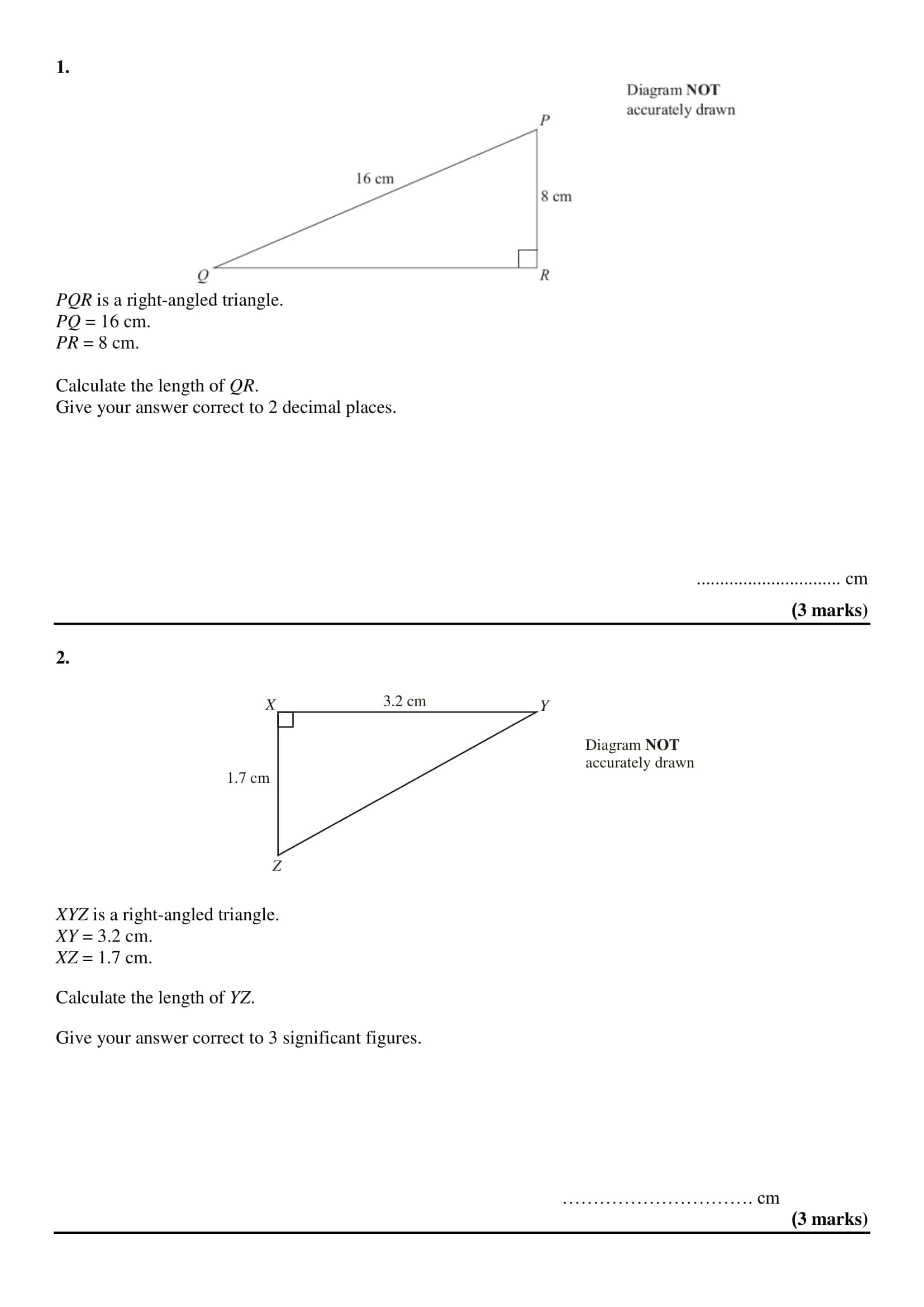
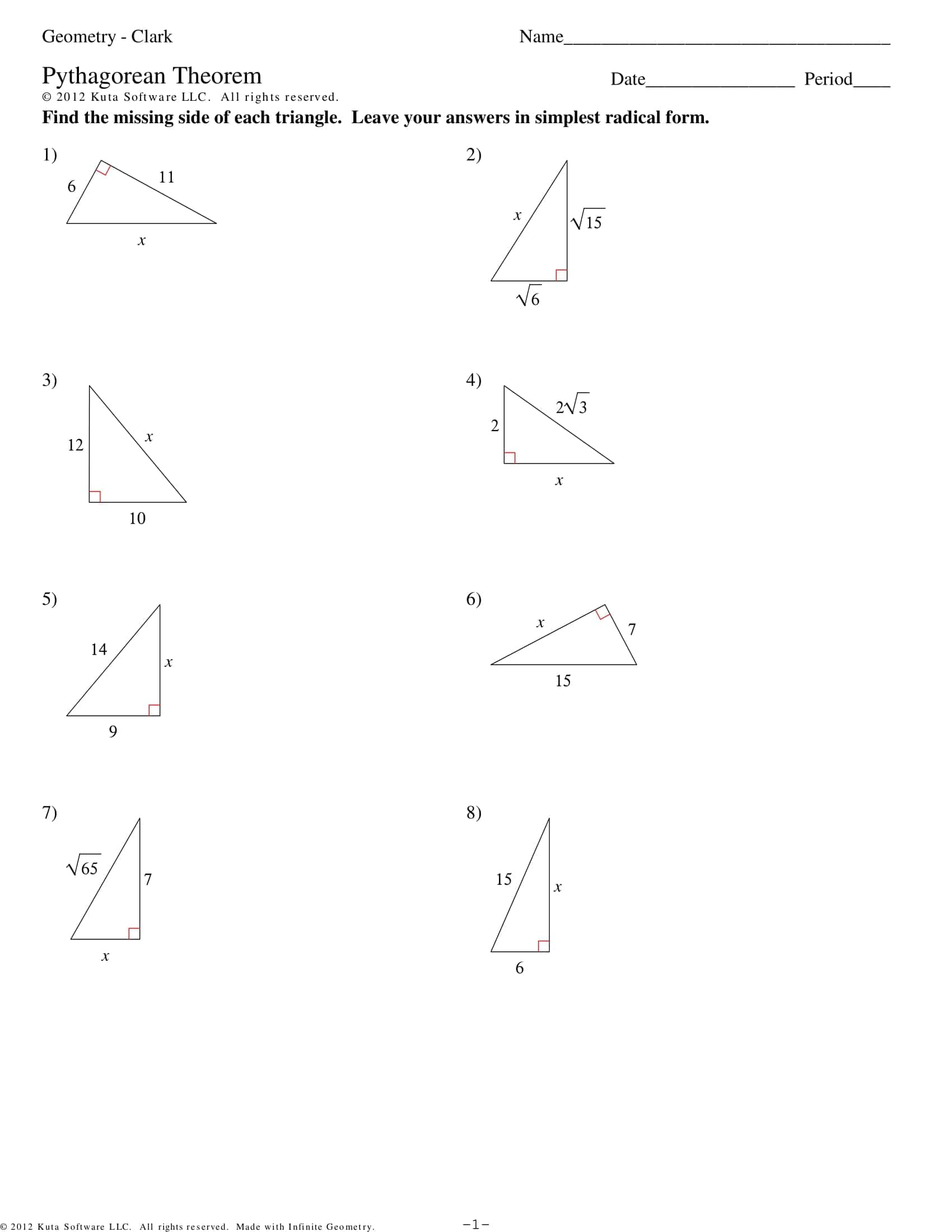
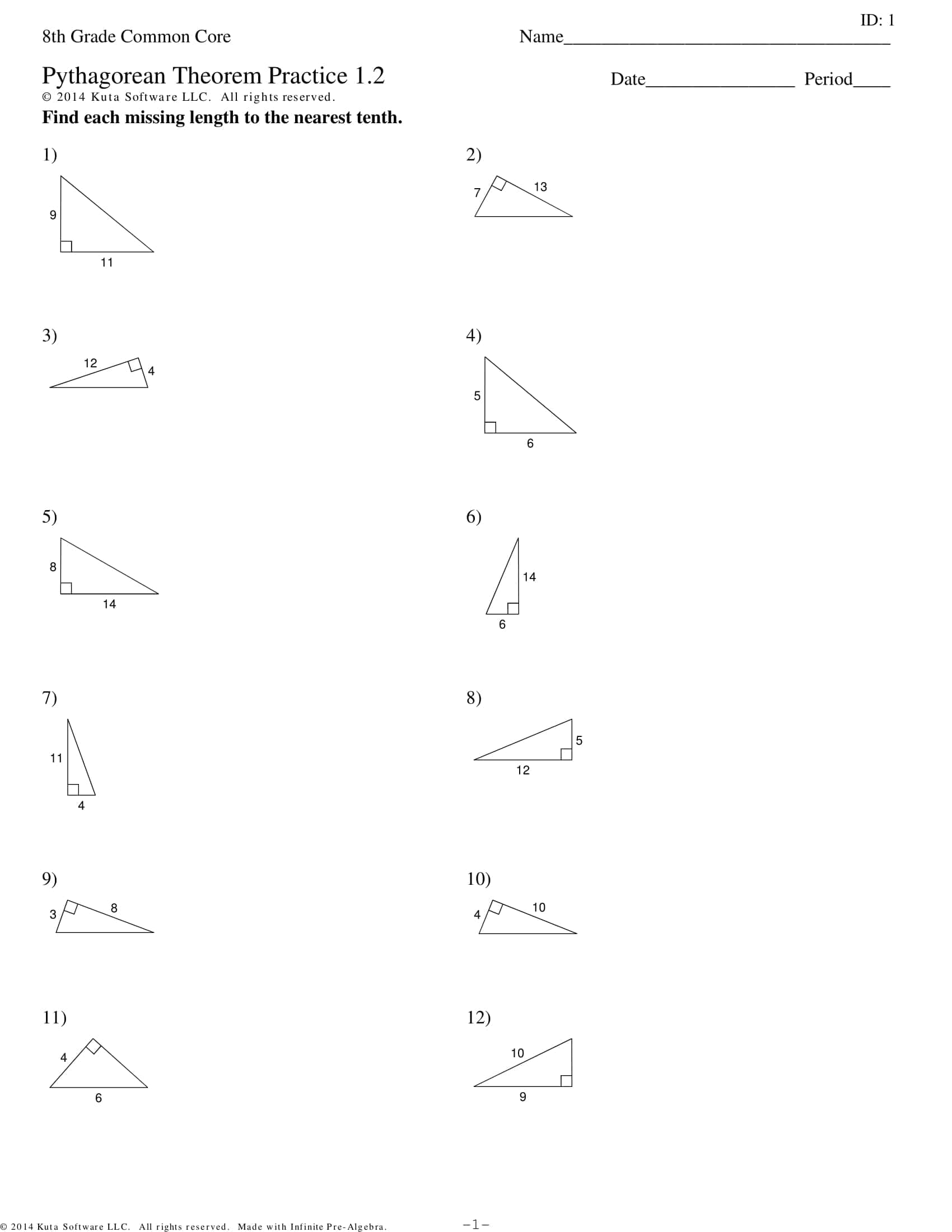
These worksheets systematically apply the leg hypotenuse relationship in a right triangle: finding the third side from two given sides, using the converse to test for a right triangle, simplifying radical results, and rounding to a specified place all with graduated progression. The TypeCalendar structure layers learning with mini notes reminding of prerequisites, sample solutions and short practices that follow immediately.
53+ Pythagorean Theorem Worksheets
Scope and Levels
The collection is divided into three difficulty tiers, with a focus on Grades 7–10:
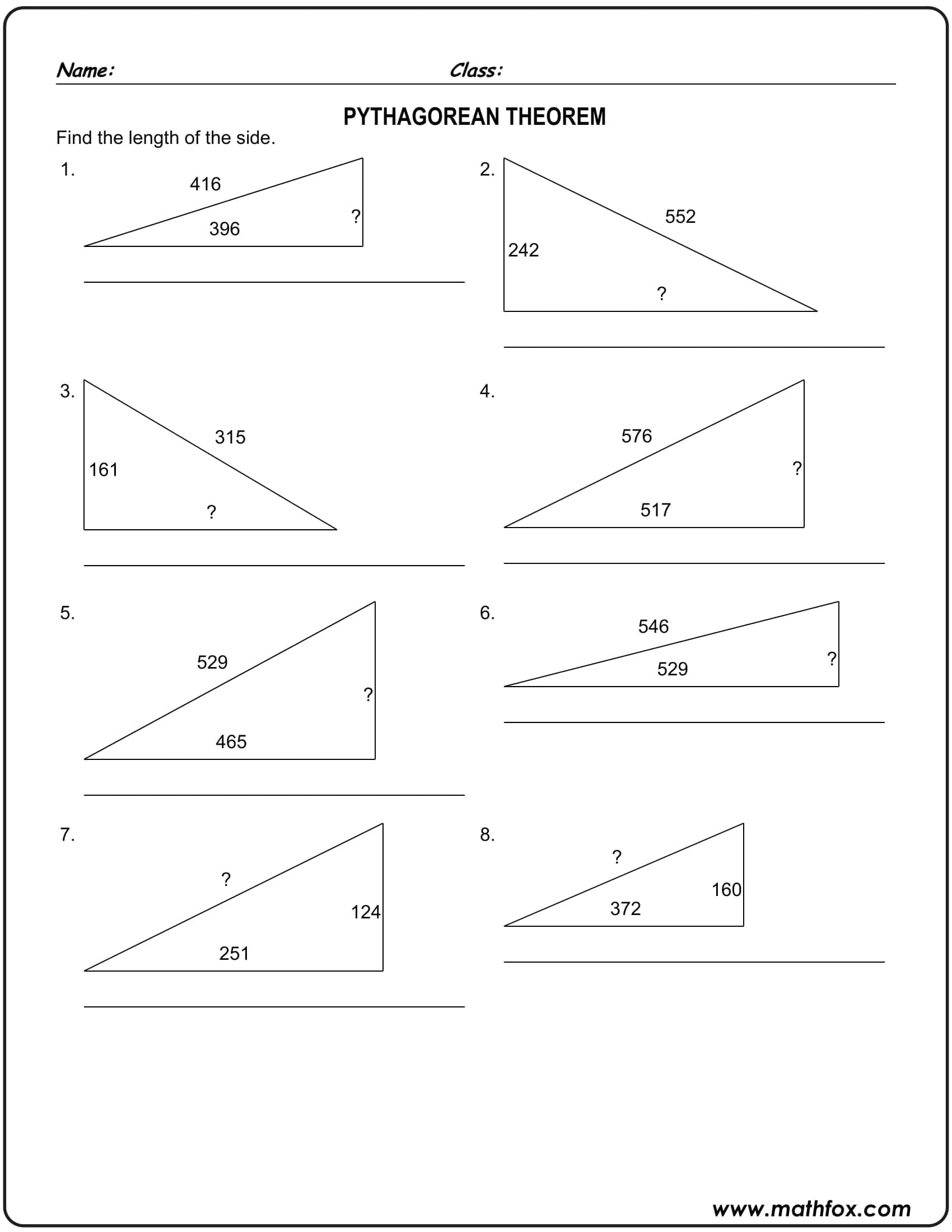
- Basic: integer sides, classic triples (3–4–5, 5–12–13), and visual grid/“counting squares.”
- Intermediate: decimal and irrational results, simplifying radicals, and conventional rounding (decimal notation).
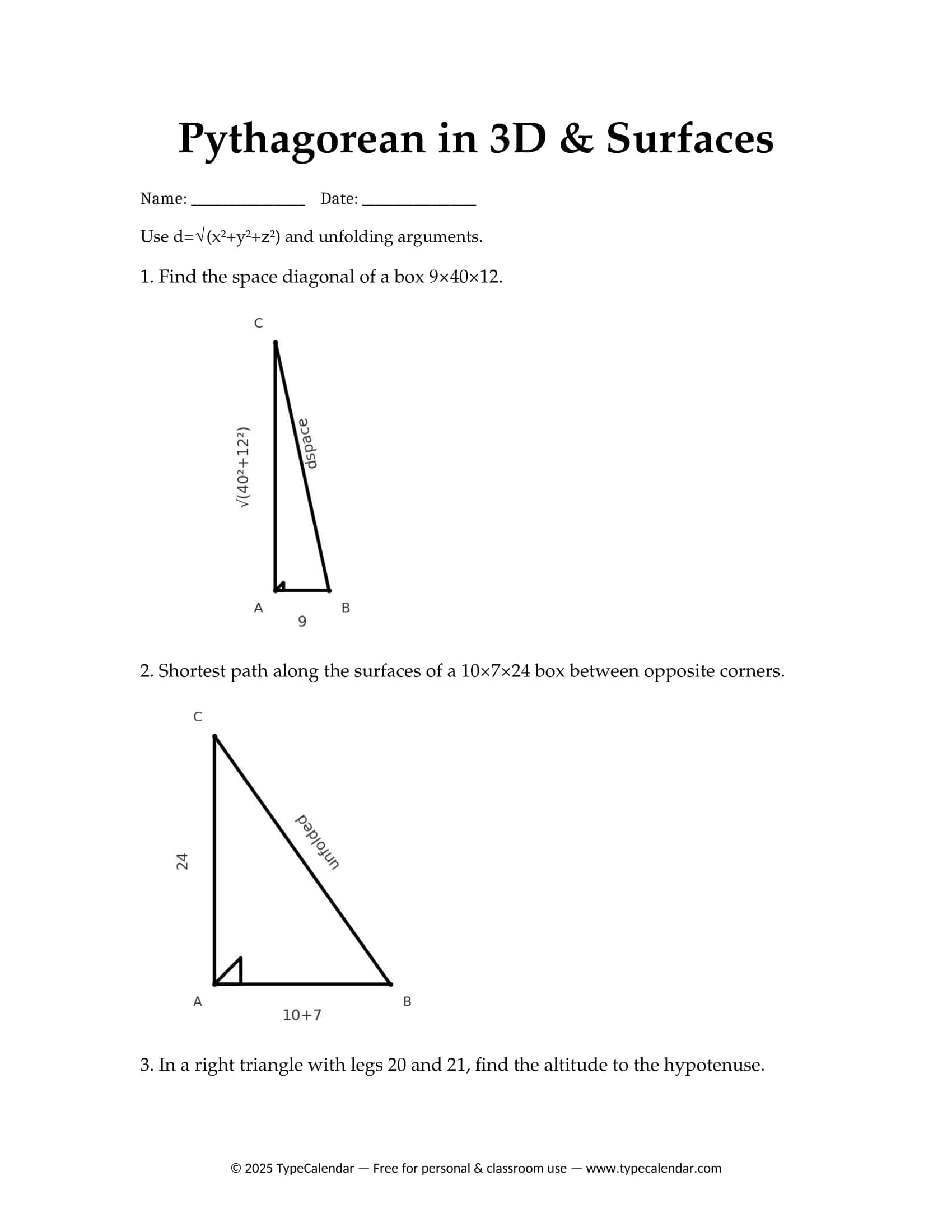
- Advanced: right triangle checks using the converse, inequality reasoning, the distance formula √[(x₂ − x₁)² + (y₂ − y₁)²], and the space diagonal of a rectangular prism.
Each section begins with a “skill label” (e.g. hypotenuse, leg, simplify radicals, distance on the plane) and recommended time, allowing teachers to easily sort pages by level.
Types of Questions and Scenarios
To make the technique permanent, the variety of questions is wide:
- Direct calculation: two sides are given and the third is asked (integer, decimal, radical).
- Converse applications: Proving whether a triangle with given three sides is right angled.
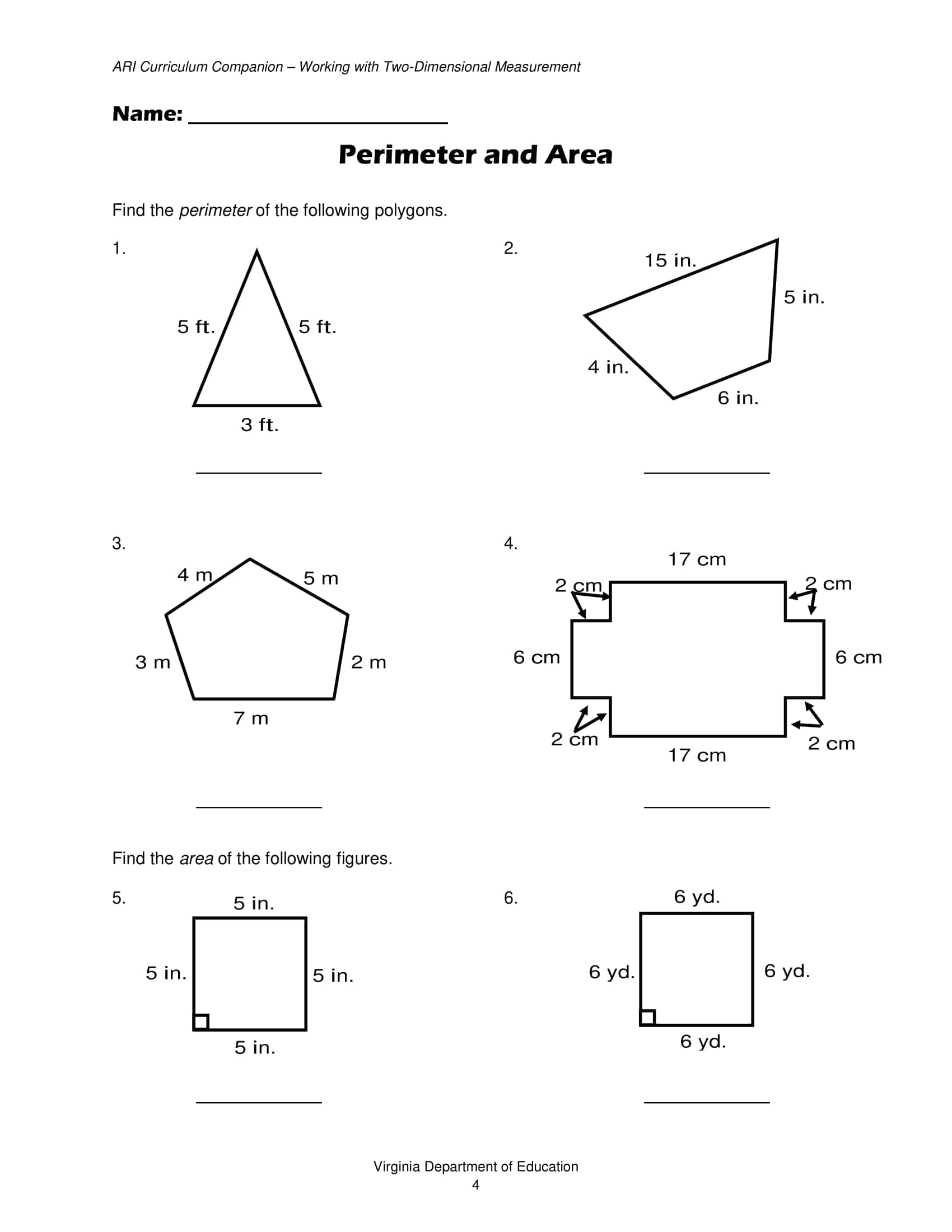
- Coordinate plane: distance between two points, multi step path problems, shortcut analysis on a grid.
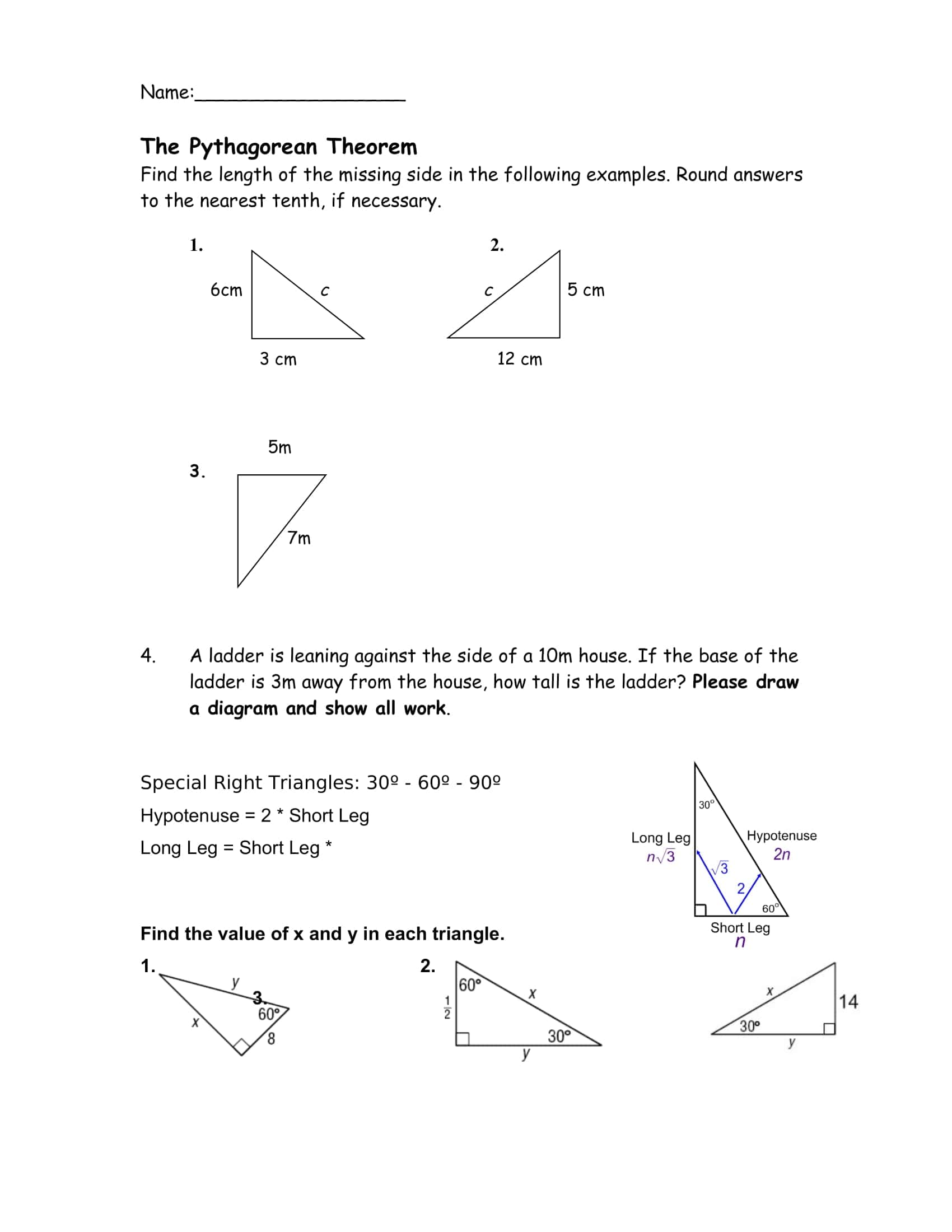
- Word problems: ladder against a wall, TV screen diagonal, rectangular garden dimensions, distance on a map/plan.
- 3B extension: finding the internal diagonal of the box, solution in two steps (base diagonal → space diagonal).
- Mixed practice: “Mini practice” pages that first make you choose a method and then make you calculate.
Classroom and At Home Use: Practical Flow
TypeCalendar pages are structured according to the warm up → target skill → mixed practice → mini exit ticket flow. The teacher; checks prior knowledge with 2–3 questions in the warm up, gives the target skill page as the main practice, sees the errors with mixed practice, and measures the achievement with a 2 question exit ticket. As homework, checkboxes let you require either an approximate decimal value or the exact radical form, so the same page fits different classes. Each PDF includes printer friendly margins, a name/date field, and a page code (e.g., PT-SetC-03), reducing versioning or copy confusion.
Download: 53+ Worksheets, Quick Response Pack
The Pythagorean Theorem is a gateway to geometry and analytical thinking; with the right set of exercises, speed and accuracy improve together. TypeCalendar’s 53+ Pythagorean Theorem Worksheet collection covers the topic from start to finish, with basic–intermediate–advanced sheets, real life scenarios, coordinate and 3D extensions, and fully solved answer keys. Download the package, choose the level, print out and with TypeCalendar turn “a² + b² = c²” from just memorization into a skill that is applied with confidence.
